62nd Annual Report on Research 2017

1. Objective of the research

The main objective of the project is to investigate the turbulence mechanisms and interactions involved in dispersed gas-liquid flows through mesoscale direct numerical simulations (DNS) and develop more general turbulence models from the simulation data to improve the predictive capability of current CFD models employed for these flows.

This report aims at analyzing the turbulent Reynolds stress budgets extracted from the mesoscale DNS data (discussed in the previous reports), and proposing a Reynolds stress turbulence model for gas-liquid flows. Moreover, the predictive capability of the proposed Reynolds stress turbulence model will be studied on a 3D bubble column by comparing it with the mesoscale DNS simulation.

2. Reynolds stress budget and analysis

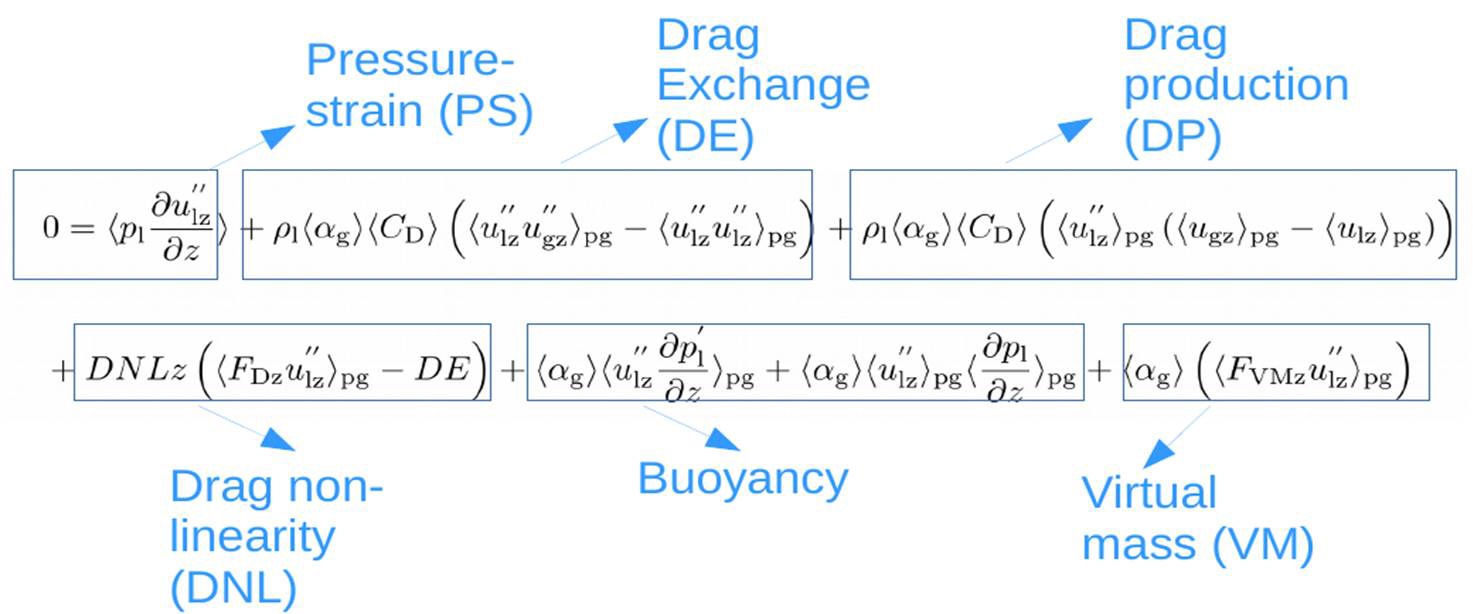
We performed a budget analysis of the different terms illustrated in Table 1, to determine their importance in the transport equation for the Reynolds stress, and to determine what terms need to be modelled.

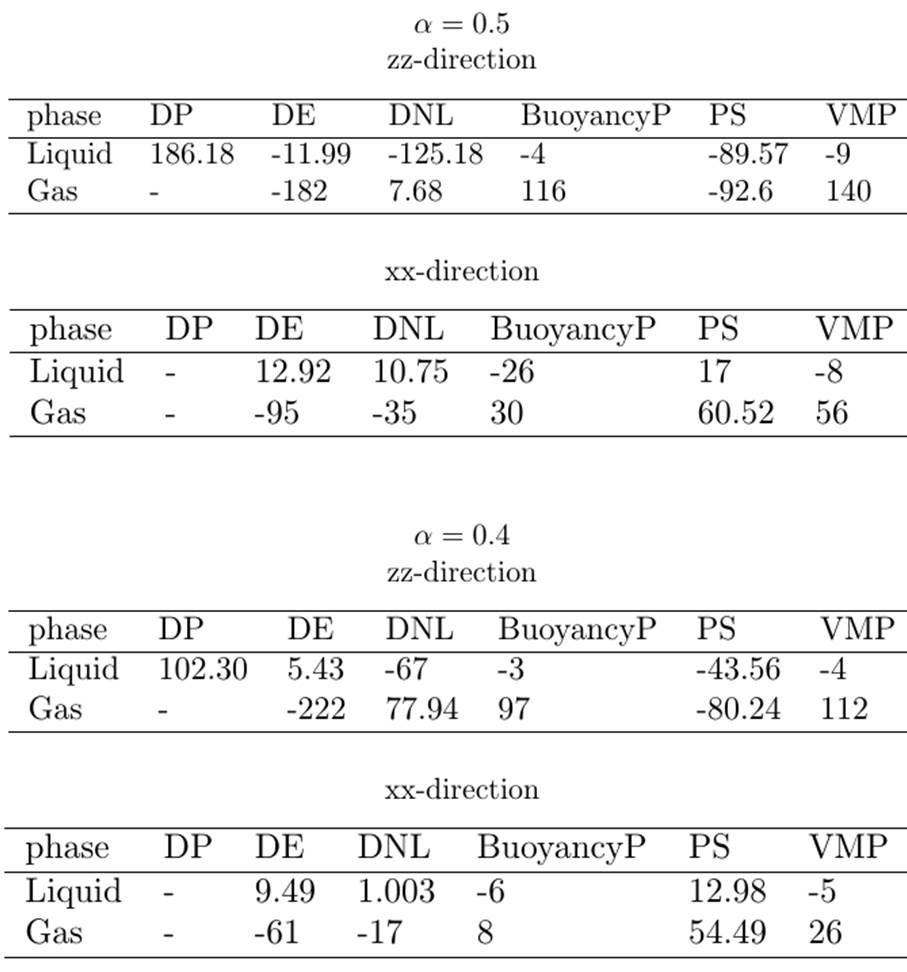
Table 2 summarizes the results obtained performing mesoscale DNS for two values of the gas volume fraction, namely 0.4 and 0.5.

Table 1. Unclosed Reynolds stress model for statistically homogeneous flows to be used as a reference to read Table 2.

Table 2. Budget for the unclosed Reynolds stress model for gas fractions 0.5 and 0.4 from mesoscale DNS

The Reynolds stress budget in the liquid phase indicate that the turbulence exchange unclosed terms (DP, DE, DNL) originated from the phase averaging of drag and the pressure strain (PS) terms contribute significantly towards the Reynolds stress budget for both the gas fractions 0.5 and 0.4. The magnitude of the terms decreases when the gas fraction is reduced from 0.5 to 0.4, indicating a negative correlation of the unclosed terms with gas fraction.

The Reynolds stress budget in the gas phase indicate that the turbulence exchange unclosed terms (DE, BuoyancyP and VMP) originated from the phase averaging of drag, buoyancy, virtual mass, and the pressure strain (PS) terms contribute significantly towards the Reynolds stress budget for both the gas loadings 0.5 and 0.4. The magnitude of the terms decreases when the gas fraction is reduced from 0.5 to 0.4, indicating a negative correlation of the unclosed terms with gas fraction.

3. Closed Reynolds Stress Turbulence (RST) liquid phase

The closure terms for the Reynolds stress model for the liquid phase considered in our work are summarized in Table 3, where the terms formulated, based on the mesoscale DNS results, are also shown.

Table 3. The RST model for the liquid phase with pressure strain, interphase production, interphase dissipation modeled from mesoscale DNS RST budget

The pressure strain (PS), inter phase production and dissipation due to the bubbles are modeled using the liquid phase mesoscale DNS budget in Table 2. The slow part of the pressure strain contribution is modeled analogous to the single phase Rotta model by modifying the time scale of turbulence and Rotta model constant to integral time scale (135tp) and C1L obtained from the mesoscale DNS simulation. The rapid part of the pressure strain is modeled in terms of Inter-phase drag production by retaining the same model constant C2L from single phase rapid pressure strain model. The interphase Production (DP) and Dissipation (DE + DNL) are modeled in terms of the slip velocity, gas fraction and drag coefficient, and the coefficient matrices as shown in Table 3 are extracted from the mesoscale DNS data in Table 2. The single models and model constants are retained for all the other terms of the RST model for liquid phase in Table 3.

4. Closed Reynolds Stress Turbulence model gas phase

The closure terms for the Reynolds stress model for the gas phase are listed in Table 4.

Table 4: The RST model for the gas phase with pressure strain, Interphase Exchange modeled from mesoscale DNS RST budget

The pressure strain (PS), Inter phase Exchange (DE) terms are modeled using the gas phase mesoscale DNS budget in Table 2. The modeling of the pressure strain in the gas phase is performed as discussed in section 2 (liquid phase RST model) by neglecting the rapid part. The interphase exchange (DE) is modeled in terms of liquid and gas phase Reynolds stresses and the model constant CDEz is extracted from the mesoscale DNS data in Table 2. The single-phase models and model constants are retained for all the other terms of the RST model for gas phase in Table 4

5. Comparison study on a bubble column

The conditions used in the numerical simulations are summarized in Table 5.

Table 5: Turbulent flow conditions

4.1. Results and discussion

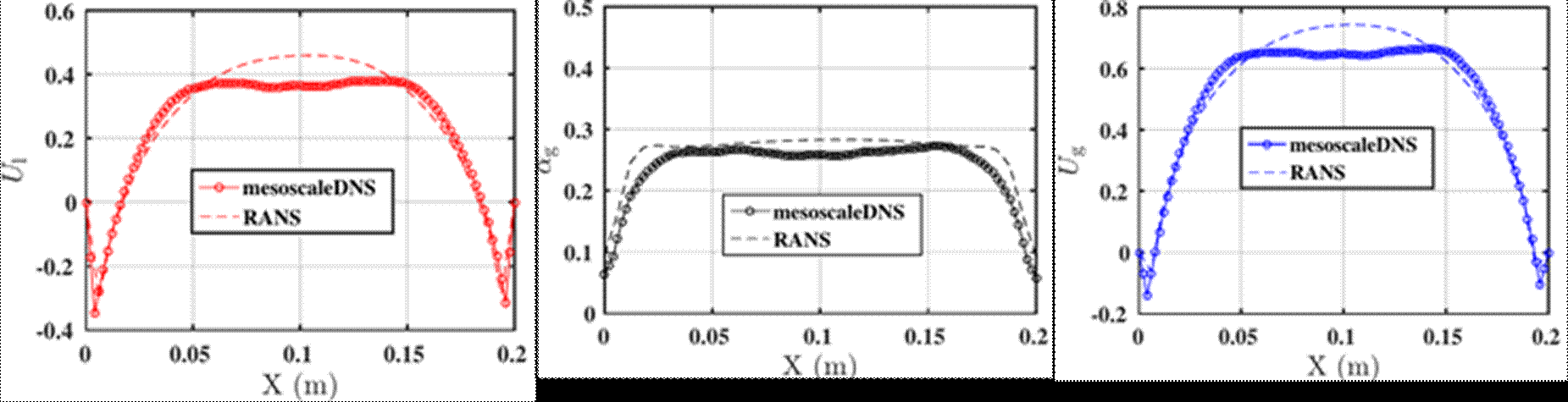
The gas fraction and velocity profiles predicted by the RANS model is comparable to the mesoscale DNS. There is a small over prediction of the velocity profiles at the center of the column (X=0.1m) which is attributed to the inability of the mesoscale DNS to capture the turbulent dissipation accurately. Hence, appropriate adjustments of the turbulent model constants in the dissipation equation must be made for both the phases to correct this over prediction. However, the prediction of the model at this stage can be considered reasonable and can be tested for more complex multiphase flows and systems. 

Figure 1. Comparison RST model with mesoscale DNS: gas fraction (Left), Liquid velocity (Centre), Gas velocity (Right)

6. Conclusions

The turbulent Reynolds stress budgets extracted from the mesoscale DNS is analyzed and a turbulent Reynolds stress model is proposed to predict turbulent gas-liquid flows. The modeling strategies involved in modeling the terms quantified through mesoscale DNS is discussed. The predictive capability of the proposed model is studied on a 3D bubble column by comparing it with the mesoscale DNS simulations. The model predictions of the gas fraction and the velocity profiles are in reasonable agreement with the mesoscale DNS. As a further study the model can be tested for more complex turbulent multiphase flows and multiphase flow systems.