Reports: UR955347-UR9: Computational Studies of Osmotic Membranes for Petroleum Wastewater Reclamation
Mingheng Li, PhD, California Polytechnic State University
| |  | |
Using
the least squares regression approach, the parameters in Equation (1) are
determined to be ![]() =
2.79 lmh/bar, k2 = 1.75×10-4 bar/(m3/h)1.67
(in the first stage), and k3 = 2.27×10-2 (m3/h)0.6/m2
(in the first stage) in order to fit the measurements under normal production
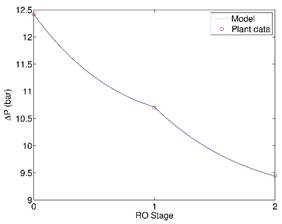
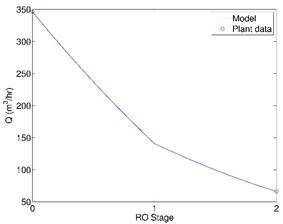
conditions in a RO plant in Southern California. The results are shown in Fig.
1.
=
2.79 lmh/bar, k2 = 1.75×10-4 bar/(m3/h)1.67
(in the first stage), and k3 = 2.27×10-2 (m3/h)0.6/m2
(in the first stage) in order to fit the measurements under normal production
conditions in a RO plant in Southern California. The results are shown in Fig.
1.
Fig. 1. Fitting of model parameters using plant data (a) transmembrane pressure and (b) flow rate.
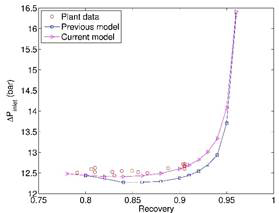
Based on the derived parameters, Equation (1) is solved under various intake flows and recoveries while maintaining the same permeate rate. The modeling results are compared with plant trial data as well as those based on an empirical model published in Desalination in 2012. While both models provide consistent and accurate prediction of transmembrane pressure at the outlet of the RO unit, Equation (1) is a little better than the previous model in predicting pump pressure and the resulting energy consumption. It matches very well with plant trial data in which the pump head is roughly constant when water recovery varies in the range of 78-90% while permeate rate is kept constant.
Fig.
2. Comparison
of current one-dimensional model incorporating CFD results (Eq. 1) with
previously published empirical model in Desalination (2012) and measurements in
a two-stage RO with a fixed permeate target. (a) transmembrane pressure
at RO inlet, (b) transmembrane pressure at RO outlet, (c) normalized pump energy
consumption.
The
results imply that the effect of concentration polarization may not be very
important in system-level modeling of large-scale industrial brackish water and
wastewater RO systems where feed salinity is low. Large flows used in these
systems greatly suppress the effect of concentration polarization, at the
expense of a high pressure drop. Moreover, these systems are typically designed
to operate far from thermodynamic equilibrium, or the transmembrane hydraulic
pressure is much larger than osmotic pressure. Because the membrane length used
in industrial RO desalination is much longer than the one typically seen in
labs, it is believed that the longitudinal variation in salt concentration is
more important than the one in the transverse direction. Therefore, Equation
(1) might serve as a good complement to concentration polarization models used
in literature for predicting and optimizing RO process performance in an
industrial setting.
Optimization
models were formulated and solved for both RO-RO and RO-PRO design
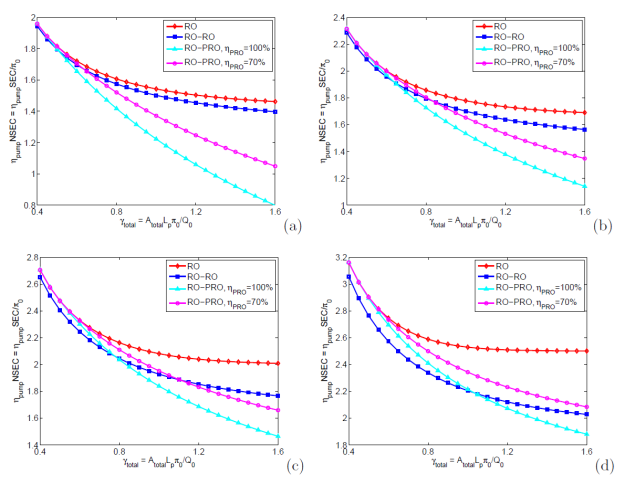
configurations shown in Fig. 3. The results of Specific Energy
Consumption normalized by feed osmotic pressure (NSEC) are presented in Fig.
4.
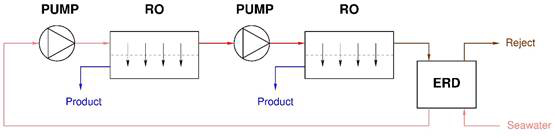
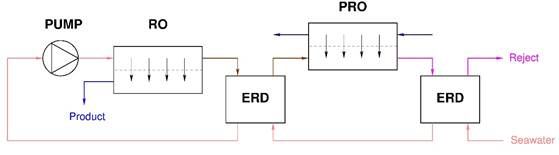
Fig.
3. Schematics
of (a) RO-RO-ERD and (b) RO-PRO-ERD.
Fig.
4. Comparison
of (NSEC) at different water recoveries (a) 30%, (b) 40%, (c) 50%, and (d) 60%.
The
results are summarized below. Both staged RO and RO-PRO configurations reduce
SEC in seawater RO desalination, provided that the membrane area is sufficient.
The latter configuration is preferred when water recovery is small, a vast
amount of membrane area is available, and the detrimental effects (i.e.
internal concentration polarization, reverse salt leakage) in PRO are not
severe. Different from hydraulic energy recovery by ERD, which has a very high
efficiency, osmotic energy recovery in RO brine by PRO can only be partially
done in a RO-PRO. Moreover, its amount is by no means close to the hydraulic
energy recovered by ERD due to the competition of areas between the RO and PRO
units. A high water recovery in RO-PRO enhances the driving force in PRO, but
reduces the feed rate at the same time, limiting the volume gain ratio on the
system level. It is expected that both methods will co-exist in the near future
until cheaper and better membranes become available.
 (a)
(a)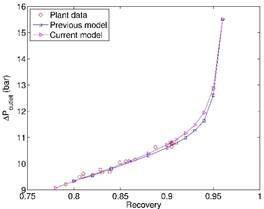 (b)
(b)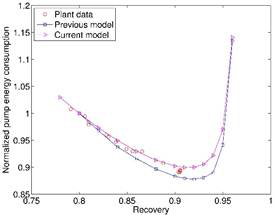 (c)
(c)