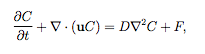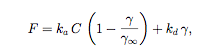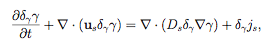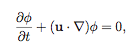Reports: ND955484-ND9: Efficient Numerical Techniques for Modelling of Surfactant-Laden Interfacial Phenomena
Petar D. Minev, PhD, University of Alberta
1. Progress in the solution of the problem and software development.
The graduate student working on the project finalized the development of the in-house code for the incompressible Navier-Stokes equation based on the high order artificial compressibility method proposed in Guermond and Minev (2017). The code was rigorously tested.
The postdoctoral fellow working on the project further developed the method for solving interface problems with surfactants. First an equation for the bulk concentration of the surfactant was added to the code. It discretizes using a direction splitting approach the following commonly used advection-diffusion equation:
where u is the velocity of the fluid, and F is the net flux of surfactant into the surface from the bulk phase modeled here by Langmuir sorption kinetics:
where and ka and kd are absorption and desorption coefficients respectively. In addition, an approximation to the equation that governs the dynamics of the surfactant on the interface:
is added to the overall discrete system. This is perhaps the most difficult part of the solution algorithm, since it requires the solution of an equation on a given interface. We followed the approach proposed by Teigen et al. (2011), that allows to transform the interface problem into a bulk problem for the concentration in a thin strip surrounding the interface. The solution to this equation is approximated by the solution of:
where δγ is a regularized δ-function with a maximum at the interface. The fluid-fluid interface is traced by a conservative version of the level set method, and the surface tension is computed in the usual for the level set method fashion (see Olson and Kreiss, 2005) solving the equation for the level set function ϕ:
where u is the velocity in the fluids domains. Then δγ is chosen as
The Navier-Stokes equations are discretized in time by a second order accurate version of the artificial compressibility method (see Guermond and Minev, 2017). The additional grad-div operator coming in the present case from the full stress formulation is split with a second order splitting discussed in Minev and Vabishchevich (submitted).
These techniques have been implemented in a Fortran 90 in-house code that is currently undergoing rigorous testing.
2. Impact on the career of the principal investigator.
The need of splitting of the grad-div operator appearing in the Navier-Stokes equations in the stress-divergence form (that is mandatory when interface problems are considered), triggered a collaboration of the principal investigator with P. Vabishchevich that resulted in a new paper (see Minev and Vabishchevich, submitted). The available software will also allow him to start a new direction of his research targeting engineering problems involving surfactant-laden interfaces. Also, the availability of a powerful parallel code that allows for simulations of surfactant-laden fluid-fluid interface problems allows the principal investigator to consider several problems of engineering interest. The principal investigator is currently on a sabbatical leave and will spend three months of it working with Prof. V. Calo from Curtin University in Australia, on the solution of such problems of interest to his group of Prof. Calo.
The postdoctoral fellow working on the project was hired for a second consecutive year to finalize the work on the software development and testing. So, this project will certainly help him in diversifying his background by learning some state-of-the-art numerical approaches to interface problems and will increase his chances for obtaining an academic or industrial position.
References:
J.L. Guermond and P. Minev, High-order time stepping for the Navier-Stokes equations with minimal computational complexity. J. Computational and Applied Mathematics, 310 (2017), 92-103.
K.E. Teigen, P. Song, J. Lowengrub, and A. Voigt, A diffuse-interface method for two-phase flows with soluble surfactants. J. Comp. Phys., 230 (2011), 375-393.
E. Olsson, G. Kreiss, A conservative level set method for two-phase flow, J. Comp. Phys., 210 (2005), 225-246.
P. Minev abd P. Vabishchevich, Splitting schemes for unsteady problems involving the grad-div operator. Submitted to: Applied Numerical Mathematics, 2017.