62nd Annual Report on Research 2017

We have recently discovered that droplets of C₁₆ alkane [CH₃(CH_­2)₁₄CH₃] suspended in aqueous C₁₈TAB [CH₃(CH_­2)₁₇N(CH₃)₃Br] solutions undergo a temperature-tunable faceting transition. Below the transition temperature (T<T_d), the droplets adopt an icosahedral shape, while still remaining liquid. These observations contrast with the behavior of classical free liquid droplets, which are always spherical. Uncovering the physics of this unique shape transition in liquid droplets is the subject of our ACS-PRF-ND funded study.

In the first year of this study, we have demonstrated that the sphere-to-icosahedron transition occurs due to the buckling of a crystalline 2nm-thick monolayer, forming at the surface of these droplets at T_s>T_d. This monolayer is composed of a co-crystallized mixture of alkane and surfactant molecules, with the interfacially-frozen structure stabilized by co-crystallization at temperatures far exceeding the bulk melting point, T_m. The crystalline packing for this monolayer is hexagonal, where the molecular coordination number is Z=6. However, such packing is incompatible with the closed surface topology, dictating the formation of lattice defects having  Z<6 coordinations. Each such defect carries a topological charge Q=6-Z, with the total charge for the whole droplet being exactly 12, by the classical Euler condition. To partly relax the tremendous lattice stretching energy associated with the topological defects, the droplets adopt an icosahedral shape at T=T_d, with a topological charge Q=1 situated at each of the vertices[1,2]

During the second year of this project, we followed more closely the dynamics of shape transitions in the temperature range T_m<T<T_d. Within this temperature range, liquid icosahedra distort along the gravity axis, forming hexagonal, parallelogram-like, and triangular platelets; more complex shapes occur occasionally as well. All these shape transitions proceed by merging of adjacent vertices of the icosahedra. Specifically, when a pair of adjacent vertices of an icosahedron merges, a hexagon emerges; tetrads of vertices merging together form a triangle. Since the icosahedra vertices bear a charge of Q=1, each vertex of the resultant hexagon carries a topological charge of Q=2; similarly, the vertices of a triangle have a charge Q=4. The parallelograms have a pair of obtuse Q=2 vertices and a pair of acute vertices of Q=4 [3]. Remarkably, the magnitude of the vertex angle decreases monotonically with the charge: higher topological charges form sharper vertices. This scaling is quantitatively reproduced by theoretical models of inextensible closed membranes, as also by simple macroscopic “kirigami” constructions, where topological defects are modeled by paper cutting and folding. The observed agreement with the inextensible membrane models’ predictions indicates that the dimensionless Fӧppl von Kármán number (Γ_νK) of the interfacially-frozen monolayer, relating its 2D Young modulus to its bending rigidity, is very high, as indeed anticipated in our previous studies[1]. The observed localization of high topological charges (Q>1), overcoming charge repulsion, is unexpected in soft matter. We are currently studying mechanisms underlying  this intriguing and unusual behavior both experimentally and theoretically. Our preliminary results suggest that the spatial distribution of topological charges across the surface of a droplet, and consequently the geometry of droplets in their platelet-like regime, strongly depend on gravity and buoyancy, suggesting that new exciting shape control methods may be developed.

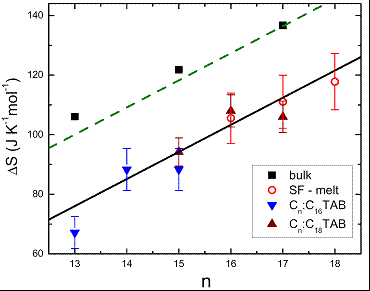
While our early droplet faceting experiments involved only the C₁₆:C_18­TAB system, recently we have extended this work to several other alkane:surfactant combinations. In particular, varying the alkyl chain lengths of both the alkane and the surfactant allows the values of T_d and T_m to be tuned. The chain length mismatch between the alkane and the surfactant has an even more dramatic influence on the faceting phenomena: when the mismatch does not allow for an efficient co-crystallization, the interfacial crystal is unstable and the droplets remain spherical down to the alkane’s melting temperature T_m­. We employed a combination of several different methods: Wilhelmy plate measurements, pendant drop technique, and a specially-devised new ‘microdroplet shape tensiometry’, to measure the interfacial tension of these droplets γ(T) over a range of values spanning several orders of magnitude[3]. From these measurements, we extracted the entropy loss ΔS_IF at the interfacial freezing transition for a range of alkane:surfactant combinations (Figure 1). The observed linear dependence of ΔS_IF on the chain length demonstrates that (only) a single monolayer of alkane freezes in all these systems; moreover, the structure of this monolayer is largely unchanged for all combinations studied. Finally these ΔS_IF values are similar to the ones detected for crystalline alkane monolayers forming at liquid-air surfaces of pure alkane melts, an effect known as `surface freezing’. Thus, similar physical mechanisms possibly play a role in both cases.

Figure 1. γ(T)-derived surface entropy loss ΔS_IF at T=T_s, for C_n:C₁₆TAB (blue down-triangles) and C_n:C₁₈TAB (brown up-triangles), matching ΔS of surface freezing in pure alkane melts (red circles); here n is the carbon number. A similar n-slope is measured for pure alkanes’ bulk freezing (squares), with these data confirming transition domination by the freezing-out of the internal molecular degrees of freedom (green dashes). Thus, a similar effect prevails for the monolayer freezing at the liquid-liquid and liquid-air interfaces.

In conclusion, our research unveiled the topological mechanisms behind the unique sphere-icosahedron and icosahedron-platelet shape transitions of surfactant-stabilized alkane droplets suspended in an aqueous surfactant solution, for several different alkane:surfactant combinations. The ACS-PRF-ND grant enabled obtaining these highly significant results and was, and still is, instrumental in training several graduate students and postdoctoral researchers, as also in developing several collaborations with theoretical teams worldwide.

References

[1] S. Guttman et al., PNAS 113, 493 (2016).

[2] S. Guttman et al., Curr. Opin. Colloid Interface Sci. 22, 35 (2016).

[3] S. Guttman et al., Langmuir 33, 1305 (2017).