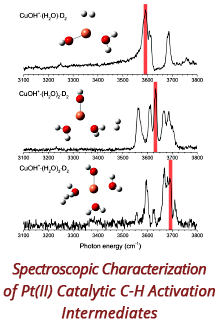
Reports: ND953240-ND9: Nonlinear electrohydrodynamics of emulsions in strong electric fields
David Saintillan, PhD, University of California San Diego
Our approach to tackling this problem has been the development of an efficient and accurate boundary element simulation code. The main advantages of using the boundary element method are accuracy and decreased computational time compared to methods based finite elements or finite differences, which require discretization of the entire fluid domain. Sherwood (1988), Baygent et. al (1998), Lac and Homsy (2007) have previously employed the boundary element method to study drops in weak electric fields. In their work they used the well-known Taylor-Melcher leaky dielectric model for the electric problem. However, they only focused on steady state deformations, and assumed convection of charges on the drop-liquid interface to be negligible and the drop shape to remain axisymmetric. Both these assumptions eliminate the possibility of observing Quincke rotation or symmetry bifurcations, which are known to occur in strong fields. The novelty in our work lies in the formulation of a boundary element method for the full Taylor-Melcher leaky dielectric model including unsteady effects and charge convection. The primary goal of our work is to solve Quincke rotation of a drop. As a first step towards that goal, we have first analyzed Quincke rotation of a circular rigid particle in two dimensions: since this problem is amenable to an analytical solution, it provides an excellent benchmark for our numerical method. Since the physical domain is 2D, the solution space is 1D i.e. the boundary integral equation is applicable on the contour of the particle. We have used cubic splines to discretize the contour, making it possible to readily extend our numerical method to non-circular or non-rigid particles, and a 4th-order Runge-Kutta time-marching scheme to advance the numerical solutions obtained by the boundary element method. A comparison with semi-analytical solutions demonstrates that the developed boundary element method is extremely accurate.
Having validated the integral formulation for rigid particles, we have then performed simulations of a two-dimensional deformable drop subjected to an electric field. The electric problem remains the same as for the cylinder while the flow problem needs to be treated differently due to deformation of the drop surface. We have first focused on weak electric fields, which has previously been studied. It is well established from previous works that the drop can exhibit two kinds of deformations contingent on the electrical parameters of the drop and surrounding liquid. Quadrupolar flow fields commonly referred to as "Taylor Vortices" are known to arise inside the drops and are indeed captured by our simulations as shown in the graphical abstract. Since, our model does not assume any axisymmetry in the drop shape, we have also been able to observe tilting of the drop upon an increase of field strength accompanied with a tank treading behavior as observed in previous experiments in the Quincke regime. However, further increase in field strength has revealed strong charge accumulation at the equatorial tips of the drops, which causes sharp charge gradients consequently triggering a numerical instability. This accumulation of charges was also confirmed by using a completely different numerical method based on level sets. We suspect this instability might be a result of the two-dimensional geometry and will be resolved in three dimensions.
Consequently, our more recent efforts have focused on the extension of our simulations to three-dimensions. In order to perform full 3D simulations of a dielectric drop under Quincke rotation, a slightly different formulation of the integral equations is needed. In a 3D domain the boundary integral equations contain singularities that do not arise in 2D or axisymmteric problems. It is well known that ignoring these singularities can lead to inaccurate solutions. Also taking derivatives of the integral equations to obtain electric field gives rise to hypersingular integrals. Very recently, we have been able to regularize the 3D boundary integral equations of the Taylor leaky dielectric model and develop an algorithm for the same. We are currently in the process of simulating Quincke rotation of a sphere using the regularized equations and comparing them to those obtained from spherical harmonics in order to validate the former method. Once the robustness of our method has been established, we plan to perform simulations of drops in both weak and strong electric fields as well as analyze drop interactions and the effect of surfactants.
From a human resource perspective, this project so far has provided one year of full support (tuition and stipend) for the PhD student who has been in charge of developing the simulation codes under the PI’s supervision at the University of California San Diego, as well as 1/2 month of summer salary for the PI.