59th Annual Report on Research 2014

Under funding from this grant we have achieved major achievements in understanding the plasticity of amorphous solids, granular flows and the glass transition. This work has led to publications in peered-review journals: two manuscripts were published in Proceedings of the National Academy of Sciences, two in Physical Review letters, two in Soft Matter, one in Europhysics Letters and one in Phys. Rev. E. The two post-doc who were funded on this grant, Gustavo During and Edan lerner, have obtained faculty positions. Gustavo During now works as an assistant professor at the Instituto de F’sica Pontificia Universidad Cat—lica de Chile. Edan Lerner is an assistant professor in the Physics department at the University of Amsterdam. Two students who participated in this project, Jie Lin and Le Yan, have both first-authored several papers in prestigious journals and will soon graduate. An undergraduate student, Alaa Saade, is second author in an EPL paper. The PI and other members of the team have been invited to several international conferences to present these works.

Our two main achievements are as follows:

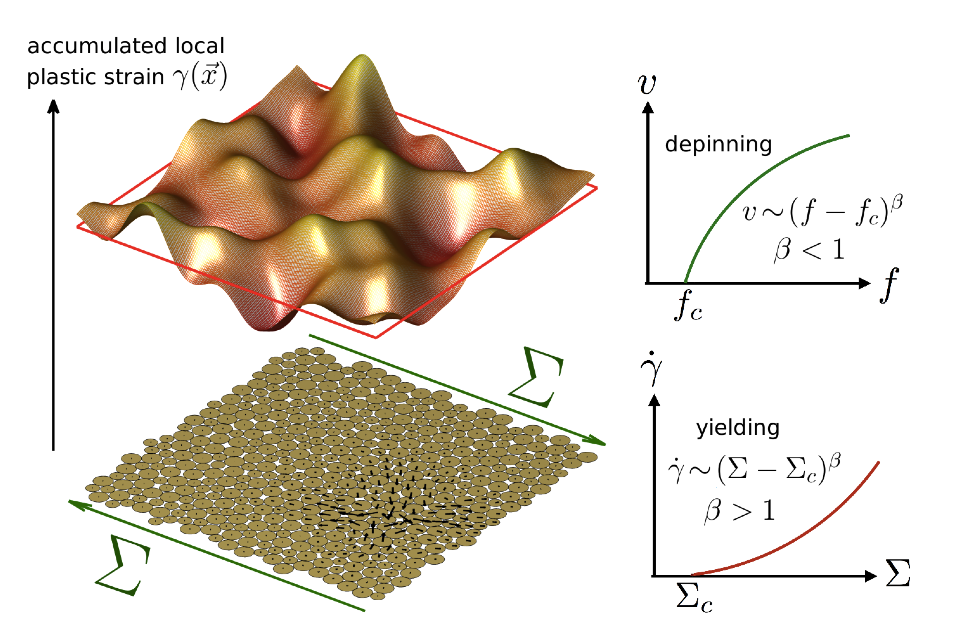
Analogy between the plasticity of amorphous solids and the depinning transition of an elastic manifold in a disordered environment.

Elasto-plasticity of soft amorphous solids: Yield stress materials flow if a sufficiently large shear stress is applied. Although such materials are ubiquitous and relevant for industry, there was no accepted microscopic description of how they yield, even in the simplest situations where temperature is negligible and where flow inhomogeneities such as shear bands or fractures are absent. Under ACS-PRF funding we have derived a scaling description of the yielding transition in amorphous solids made of soft particles at zero temperature. Our description made a connection between the Herschel-Bulkley exponent characterizing the singularity of the flow curve near the yield stress, the extension and duration of the avalanches of plasticity observed at threshold, and the density of soft spots, or shear transformation zones, as a function of the stress increment

beyond which they yield. We showed that the critical exponents of the yielding transition can be expressed in terms of three independent exponents, characterizing respectively the density of soft spots, the fractal dimension of the avalanches, and their duration.

Our description built a strong connection with the depinning transition that occurs when an elastic manifold is driven through a random potential, as represented in Fig.1. Overall, we provided a novel way to think about this important practical problem, building bridges between different disciplines. Our analysis may help to create new amorphous materials with desired rupture properties.

Left:  floppy spring network sheared near a shear-induced jamming transition. Red links indicate springs under tension, black links indicate springs under compression. Right: Contact network made by hard particles in a viscous flow of a dense suspension. Black segments indicate contact forces between particles. The two networks have very close geometrical properties, an analogy that enables to derive many properties of dense suspensions.

Rheology of dense non-Brownian suspensions: rheological properties of dilute suspensions are well known since the early works of Einstein and Batchelor. Their behavior in the dense limit remains mystifying however, and of critical importance for the industry: it is central to the manufacture of materials and their applications, and to the understanding of slurries and oil sand. As the packing fraction of particles increases, particle motion becomes more collective, leading to a growing length scale and scaling properties in the rheology as the material approaches the jamming transition. There was a knowledge gap on this question, and no convincing microscopic description of this phenomenon. One the other hand, in recent years it had been understood that the elasticity of simple amorphous solids was governed by a critical point, the unjamming transition where the pressure vanishes, and where elastic properties display scaling and a diverging length scale. The correspondence between these two transitions was however unclear. Under ACS-PRF funding we established a formal analogy between the rheology of the flow and the elasticity of simple networks. Recently we used this analogy to compute the length scales that characterize the dynamics in dense suspensions, thus solving a long-standing debate in the field. 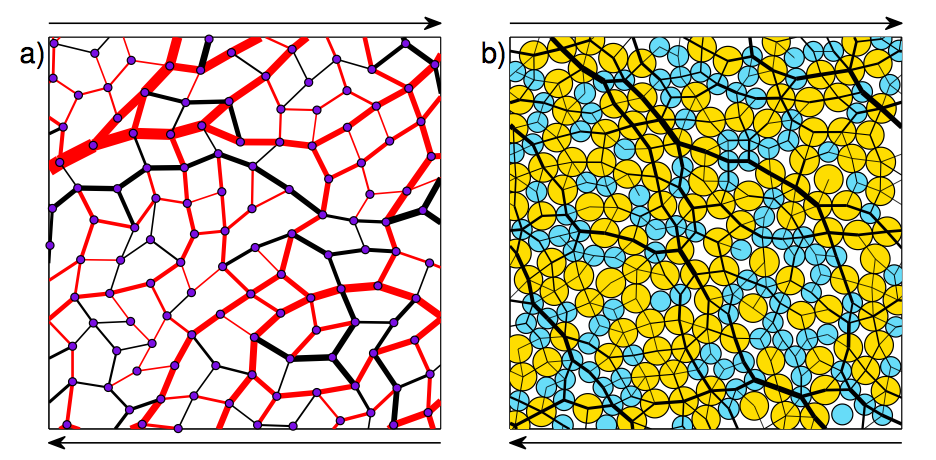We found that the length scale in the fluid phase is related to the length scale that appears in certain elastic properties of the solid phase, which diverges near the unjamming transition where flow starts. Fig.1 illustrates this analogy: one observes the contact force network generated between moving particles in flow, which is very similar to force chains observed in elastic network as shown on the left. This analogy, together with analytical technics to study the elasticity of network, led to these new conclusions.  Potential applications concern the design of materials such as slurries, emulsions, and many other particulate materials with desired rheological properties.