59th Annual Report on Research 2014

The JKD dynamic permeability model of Johnson and co-workers offered the first scaling relationship to model the frequency-dependence of permeability. It relies on a single free parameter, the rollover frequency ω_c, which depends on fluid and matrix properties. This critical frequency represents the transition from viscous to inertia-dominated momentum balance in a homogeneous porous medium. Additionally, Smeulders and co-workers provided a rigorous mathematical validation of the model using homogenization methods (Smeulders et al., 1992).

In this study, we investigate different porous media topologies and their effect on the dynamic permeability to verify the scaling of the JKD model. We observe that the dynamic permeability response is generally in good agreement with the scaling proposed by Johnson et Smeulders (Johnson et al., 1987; Smeulders et al., 1992). However, in specific cases, we observe a significant departure from the JKD model. In particular we observe features to suggest a resonance behavior. First, using a continuum scale argument, we discuss the importance of a correction term to Darcy's law for transient flows that allows us to derive a hyperbolic version of the mass conservation equation. Although this continuum-scale model offers a satisfying framework to explain the occurrence of resonance in one medium, it fails to explain the lack of resonance in the three other media. Alternatively, we suggest that pore-scale effects, such as different pore-size distributions (PSD) can also facilitate pore pressure excitation between heterogeneous flow pathways in response to forced pore-pressure excitations.

Numerical model and Results

Our pore-scale flow simulations are based on the lattice Boltzmann method to compute the 3-D flow field at the pore scale in each medium and calculate the static permeability as well as the temporal evolution during many pressure cycles to calculate the dynamic permeability.

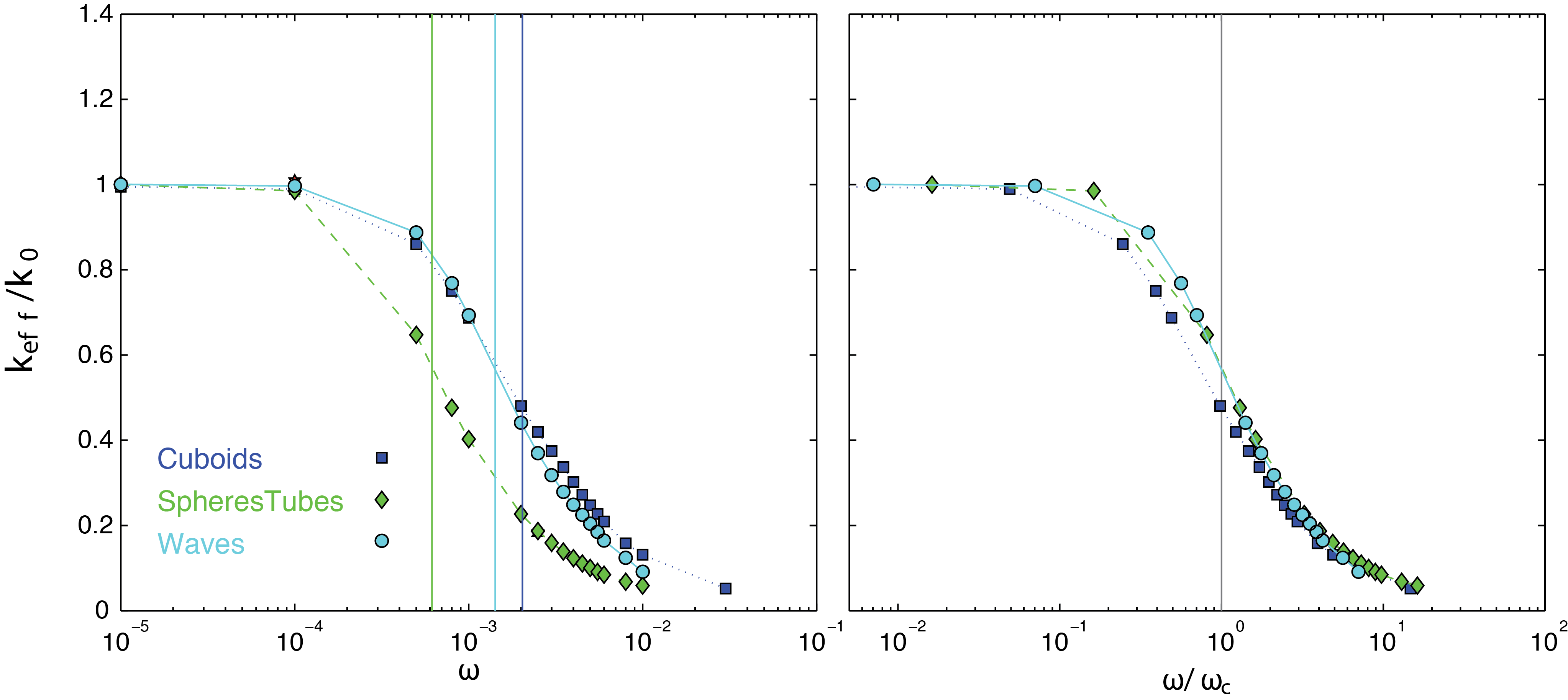
In Figure 1a, we show the un-normalized results for three of the four media. We can clearly observe similar trends with a sudden decay of effective permeability as the forcing frequency approaches the critical frequency of each medium w_c. Once the frequency is normalized w_c (Fig. 1b) the data collapses as expected for the self-similar trend observed and documented by several authors (Johnson et al., 1987; Smeulders et al., 1992).

Figure 1. Effective (dynamic) permeability as function of frequency for three of the four porous media used in this study.

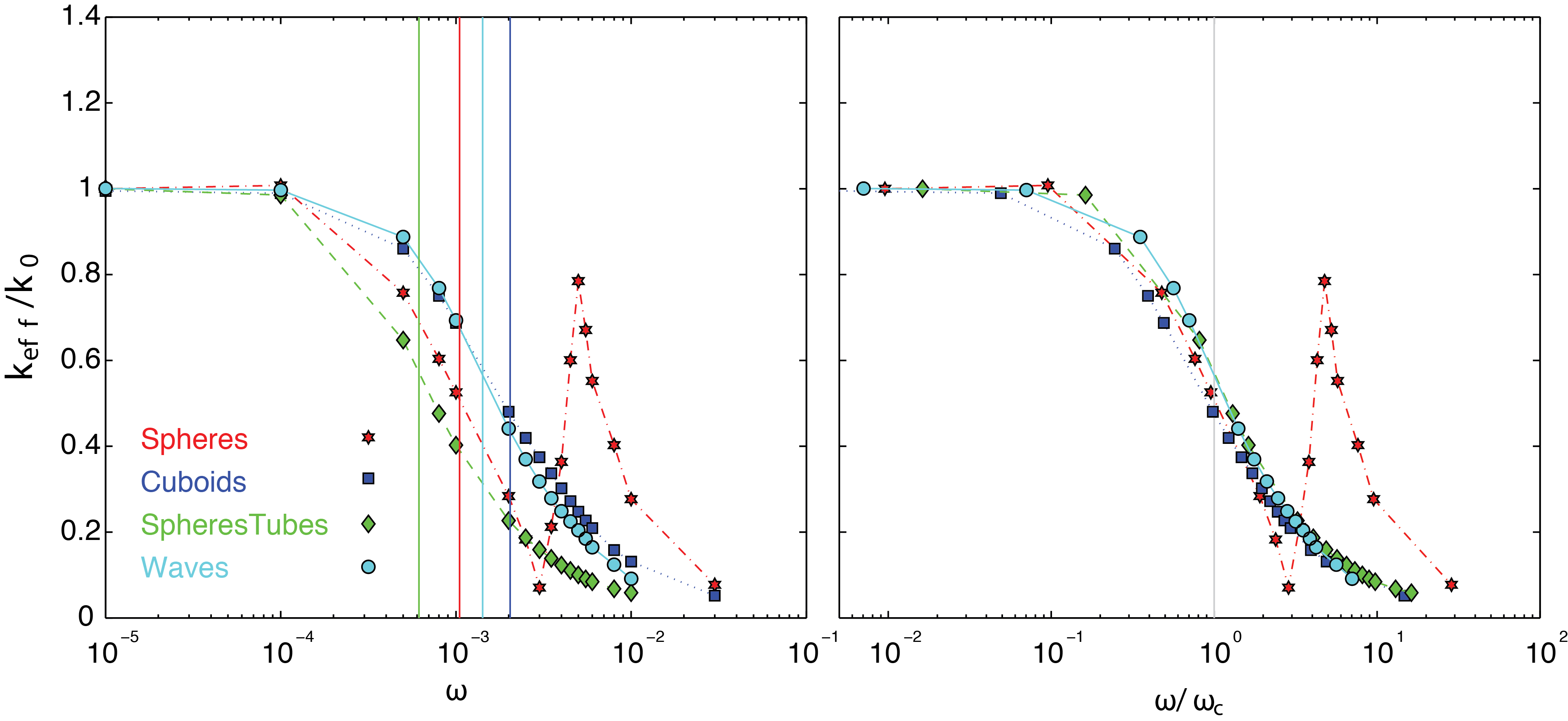
We conducted the same simulations on the porous medium with broader pore-size distribution and obtained a significantly different result (Fig. 2). The existence of a permeability peak at high frequency is unexpected from the existing theory and suggests a resonance-like behavior over a narrow range of forcing frequencies.

Figure 2. Same as Figure 1 but with the last porous medium.

In reality, we know that it will take a finite time for pressure to propagate a finite distance in a porous medium. It is therefore necessary to introduce a transient term to modify Darcy's equation. Doing so, we retrieve a simple hyperbolic Telegraph equation

(1)

If the relaxation time τ≪1, then the parabolic groundwater flow equation is retrieved. One can directly conclude that this hyperbolic equation admits the propagation of damped waves that travel with a finite velocity c = (K_fF/ρ_f)^1/2, where we identified the relaxation time τ with ρ_fk₀/η = 1/ω. This means that our model is consistent to that of JKD where the transition between inertia and viscous dominated regimes occurs around the rollover frequency ω_c. Equation (1) admits resonance and predicts a peak around the resonance frequency observed in Figure 2. However, it also predicts that the other porous media are capable of producing resonance peaks, which is not compatible with our numerical results.

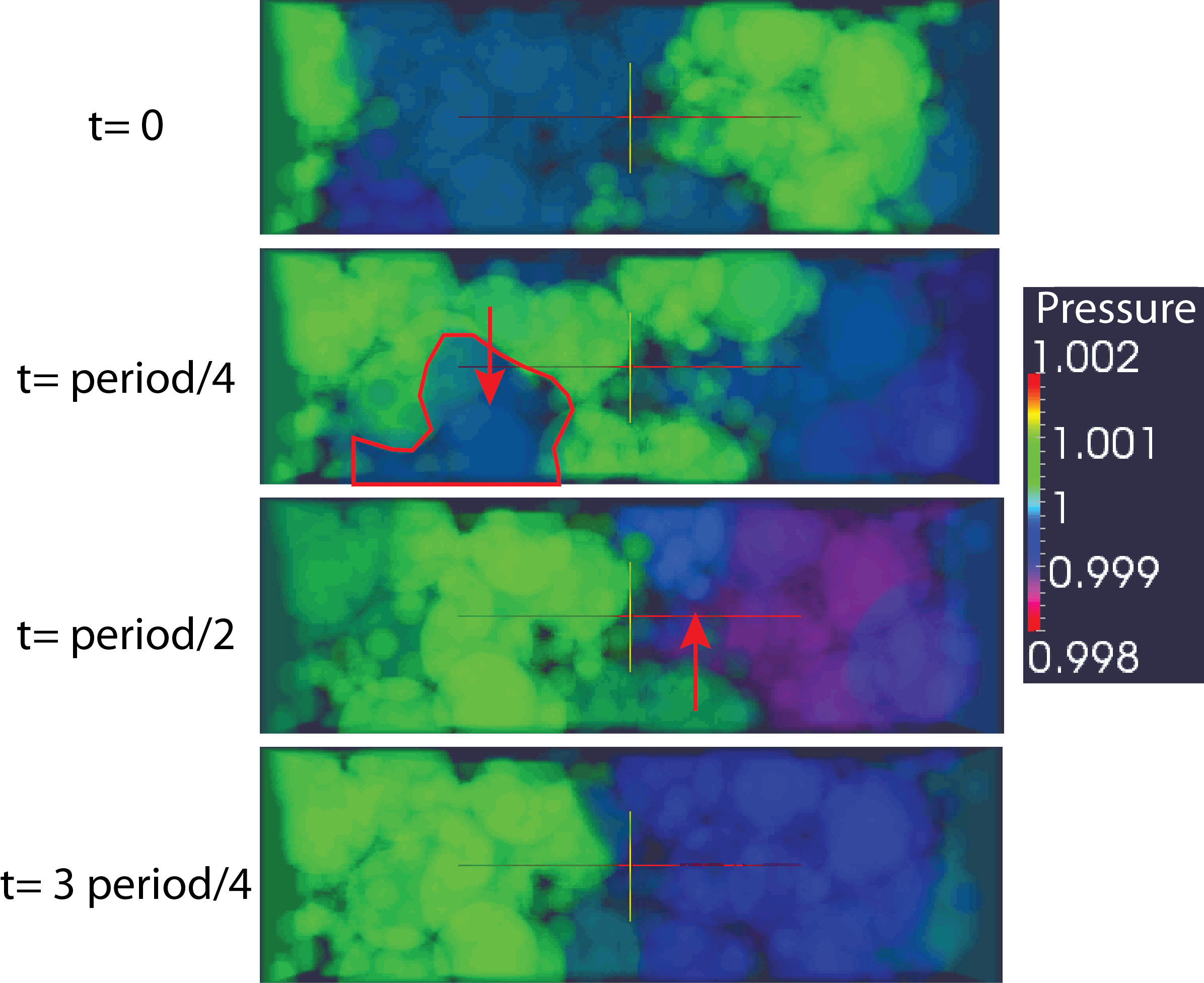
Alternatively one can argue that pore-scale processes control the existence of the resonant peak. Figure 3 shows snapshots of the pore-pressure field in this medium and shows pressure waves propagating from the outlet into the medium. A possible explanation for the resonant behavior is that the heterogeneous porous medium can be viewed as a collection of connected primary and secondary pathways for the fluid percolation and by extension pressure wave propagation. One clearly observes from Figure 3 that pressure fluctuations can propagate further into the medium along the main flow pathways forming some important pressure gradients perpendicular to the main flow direction between connected pathways with different transient responses to stress propagation.

Figure 3. 3-D visualization of the pore-pressure field (normalized). Note the regions with large lateral pore pressure gradients (the imposed gradient is left to right) highlighted in red. It shows that flow pathways with different hydraulic connectivity have different response time to the transient forcing.

The resonant behavior may be associated with the existence of a finite time-delay for the pore pressure to relax between connected primary and secondary pathways at a given distance from the imposed forcing. If the response time for the pore pressure exchange between these different connected pathways approaches the period of the forcing, we argue that resonance may occur. However, because these features in the Spheres medium are sub-REV, a continuum-scale 1-D model such as the one presented above may not appreciate these effects.