59th Annual Report on Research 2014

Supercritical fluids possess properties between those of liquids and of gases. Peculiar properties of fluid mixtures in the vicinity of the critical point of the pure solvent are commonly used in supercritical-fluid technologies, such as fluid extraction, enhanced oil recovery, supercritical chromatography, and micronization. These properties are linked to critical-point anomalies, in particular, very large compressibility and very low interfacial tension. Water, near its vapor-liquid critical point, as a supercritical solvent, is well studied, in contrast to supercooled water. However, more recently, many scientists have started to believe that deeply in supercooled region, not directly accessible to bulk-water experiments, there exists a critical point of liquid-liquid separation (“liquid water polyamorphism”). In this project the search for water’ polyamorphism was performed water through investigation of aqueous solutions well below the freezing point of pure water. The proposed idea was that, if the water liquid-liquid critical point exists, the addition of a solute would generate critical lines emanating from the pure-water critical point. The phenomenon would be conceptually similar to what is known near the vapor-liquid critical point and what is commonly exploited in supercritical-fluid science and technology. 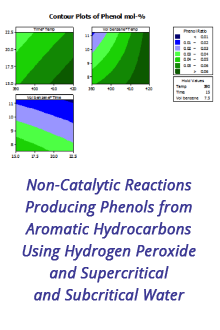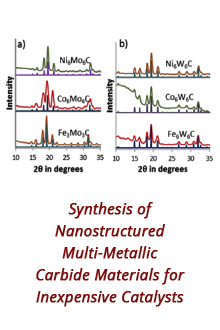The investigation of aqueous systems below the freezing temperature of pure water would not only shed light on the nature of plausible water polyamorphism, but also could open the way for utilizing cold water as a novel and unusual supercritical-fluid solvent.

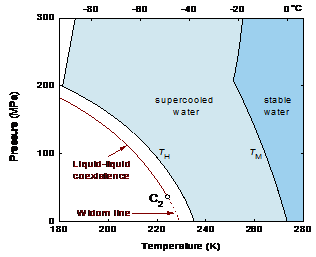
Figure 1. Hypothetical phase diagram of cold water. T_M is the melting line. T_H is the line of homogeneous ice nucleation. The location of the liquid-liquid coexistence curve is sketched as suggested by Mishima, The suggested location of LLCP (C₂) is about 30 MPa. The continuation of the liquid coexistence curve into the one-phase region is the line of maximum fluctuations, the Widom line.

If the metastable liquid-liquid transition in water exists (and if it is terminated by a critical point), the addition of a solute should generate a line of liquid–liquid critical points emanating from the critical point of pure supercooled water. We have analyzed thermodynamic consequences of this scenario. In particular, we consider the behavior of two systems, H2O-NaCl and H2O-glycerol. We have found the behavior of the heat capacity in supercooled aqueous solutions of NaCl to be consistent with the presence of the metastable liquid–liquid transition. We have elucidated the non-conserved nature of the order parameter (extent of “reaction” between two alternative structures of water) and the consequences of its coupling with conserved properties (density and concentration). It has been also shown how the shape of the critical line in a solution (the so-called “Krichevskii parameter”) controls the difference in concentration of the coexisting liquid phases.

To developed thermodynamics of aqueous solutions it was assumed that liquid water is a "mixture" of two states, A and B, of the same molecular species. For instance, these two states could represent two different arrangements of the hydrogen-bond network in water and correspond to the low-density and high-density states of water. The fraction of water molecules, involved in either structure, is controlled by thermodynamic equilibrium between these two structures. Unlike a binary fluid, the fraction is not an independent variable, but is determined as a function of pressure and temperature from the condition of thermodynamic equilibrium. The critical temperature is to be specified through the temperature dependence of the equilibrium constant.

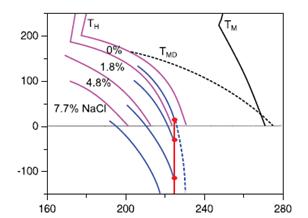
Figure 2. Suggested Pressure (MPa)-Temperature (K) phase diagram for supercooled aqueous solutions of sodium chloride exhibiting liquid–liquid transitions hidden by homogeneous ice formation. Solid pink curves show homogeneous ice formation T_M labels the equilibrium melting temperatures and T_DMthe maximum density temperatures.

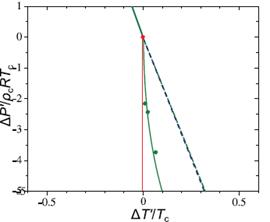
Figure 3. A comparison of the proposed equation of state with the simulation results of Corradini and Gallo for the TIP4P model The green solid line and green dashed line show a linear approximation of the LLT and Widom line for the TIP4P model. Green circles show the critical points calculated at different mole fractions of NaCl in simulation, while the red line shows the critical line for the equation of state. The critical point of H2O is shown as a red circle. The data of Corradini and Gallo re-scaled so that the LLT has the same slope as in real water.

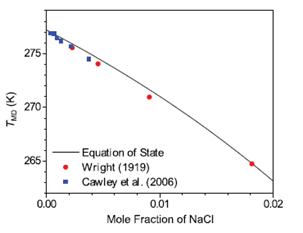
Figure 4. Temperature of maximum density in aqueous solutions of supercooled water. The black line shows the equation of state developed in this project, while the red squares and blue circles show the measurement results.

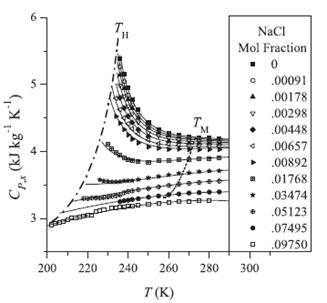
Figure 5. Suppression of the anomaly of the heat capacity in aqueous solutions of sodium chloride. Symbols: experimental data of Archer and Carter. Solid curves: predictions based on two-state thermodynamics. Dashed curve shows the positions of the melting temperatures Dashed-dotted curve shows the temperatures of homogeneous ice formation.

The results of comparison between the developed theory and available experimental and simulation data are shown in Figures 2 through 5. The agreement between the theory and experiment is remarkable. Thus we have confirmed that the existing experimental and simulation data on supercooled water are consistent with the concept of water’s polyamorphism.

We also report the results of a computer simulation study of the thermodynamic properties and the thermal conductivity of supercooled water as a function of pressure and temperature using the TIP4P-2005 water model. The thermodynamic properties are represented by the two-structure equation of state consistent with the presence of a liquid-liquid critical point in the supercooled region. The simulations confirm the presence of a minimum in the thermal conductivity, not only at atmospheric pressure, as previously found for the TIP5P water model, but also at elevated pressures. This anomalous behavior of the thermal conductivity of supercooled water appears to be related to the maximum of the isothermal compressibility or the minimum of the speed of sound. However, the magnitudes of the simulated thermal conductivities are sensitive to the water model adopted and appear to be significantly larger than the experimental thermal conductivities of real water at low temperatures.