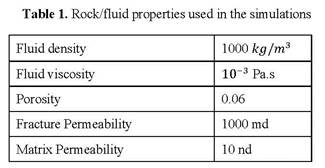
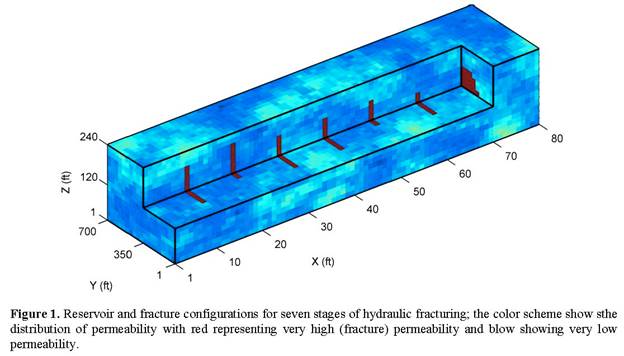
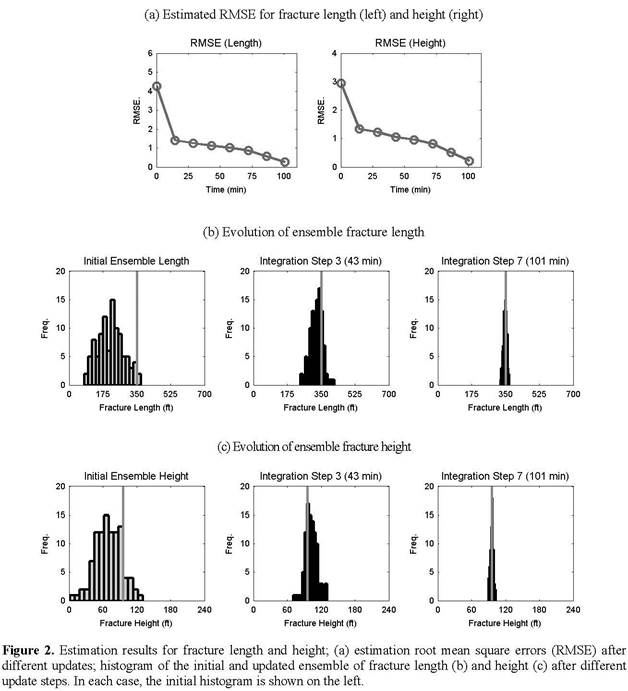
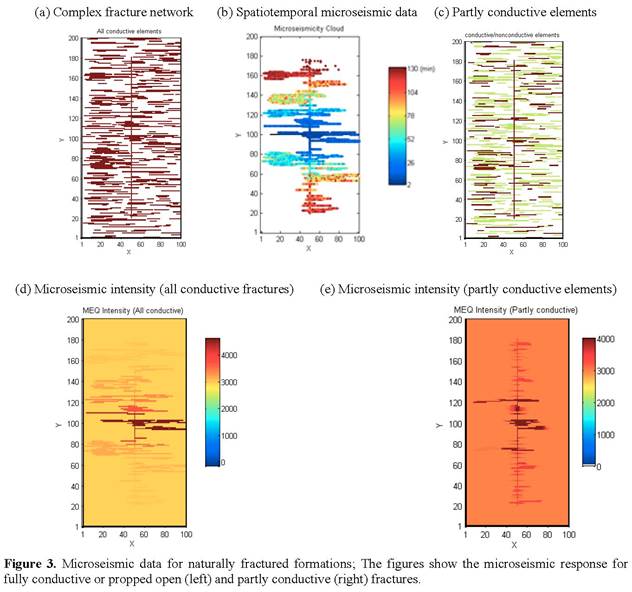
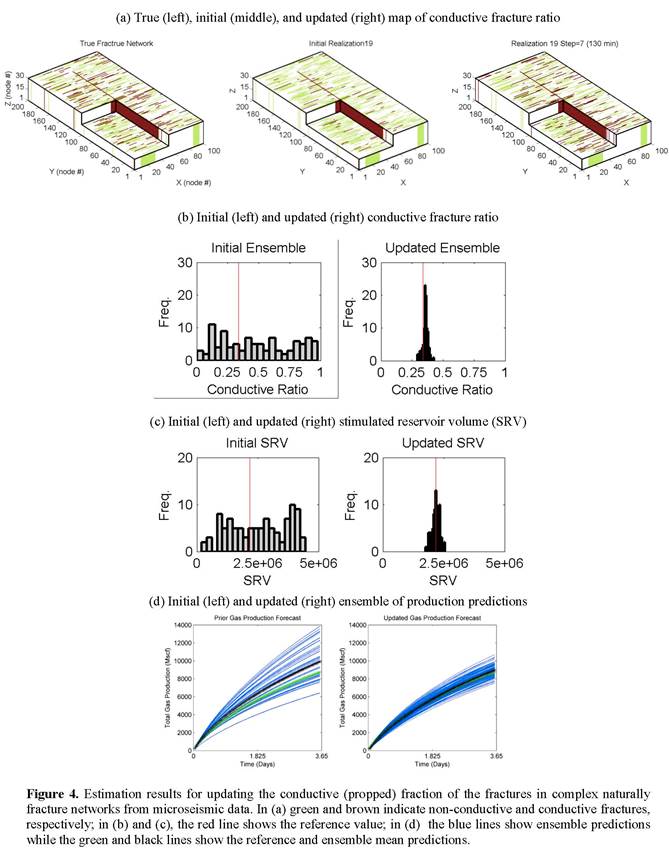
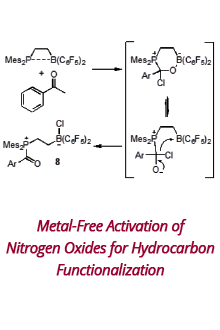
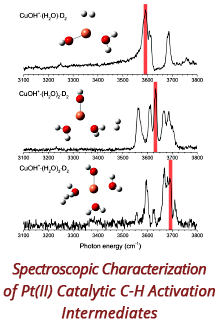
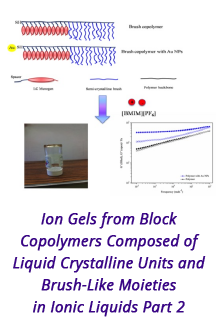
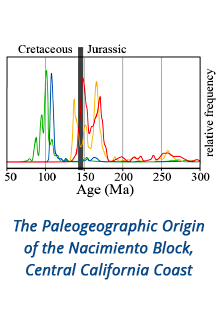
Reports: ND952864-ND9: Prediction of the Stimulated Reservoir Volume and Production Performance in Unconventional Reservoirs from Monitoring Observations of Coupled Thermal, Geomechanical and Transport Processes
Behnam (Yousef) Jafarpour, PhD, University of Southern California
![]()