Reports: UR551889-UR5: Fundamental Simulations of Jamming in Confining Geometries: Effects from Surfaces, Obstacles and Exits
Amy L. Graves, PhD, Swarthmore College
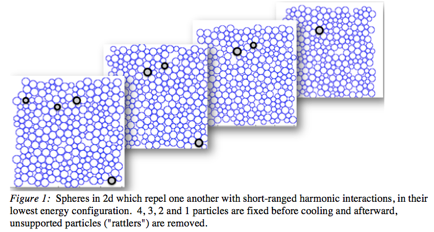
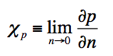
![]()
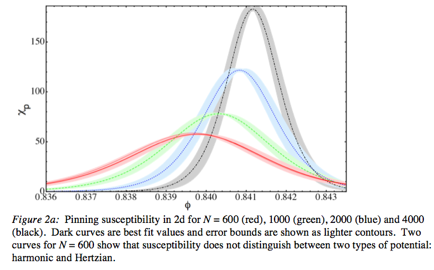
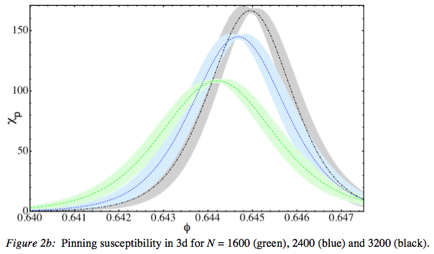
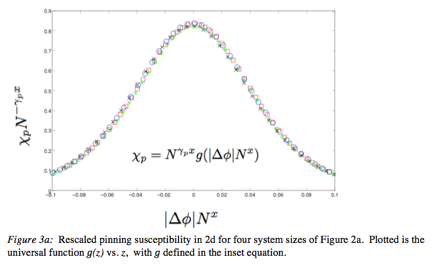
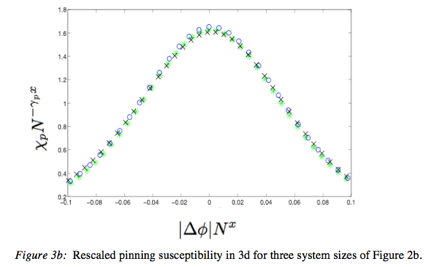
![]()
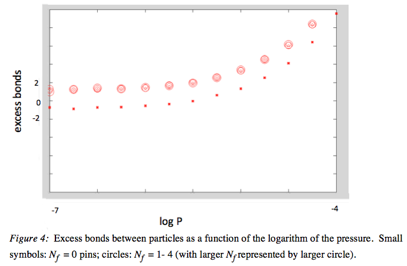
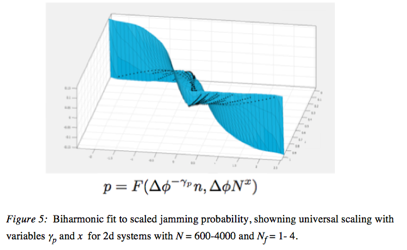
Amy L. Graves, PhD, Swarthmore College

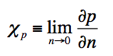
![]()




![]()


Copyright © American Chemical Society