59th Annual Report on Research 2014

Summary and Impact

We seek a thorough understanding of flows of wormlike micelles (WLMs) in realistic processing flows, including instabilities such as shear banding. In FY2013, we identified that complex drag flows of WLMs (as in a four-roll mill device) were dominated by the emergence of highly localized high-shear bands near the moving surfaces, which paradoxically enhanced extensional components of the flow away from these surfaces. This suggests that complex flows of wormlike micelles are highly dependent on shear banding effects near surfaces. In such cases, surface curvature should play an important role in determining the macroscopic flow.

In FY2014, we focused on systematically studying the impact of geometry curvature on the development of shear banding flows. To do so, we acquired a customized rheometer for velocimetry measurements (rheo-PIV) in concentric cylinder (Taylor-Couette) flow. We modeled the flows using a physically realistic rheological model for WLMs, the Vasquez-McKinley-Cook (VCM) model. Increasing curvature leads to an expansion of the envelope of critical shear rates for banding, as predicted by the VCM model. Furthermore, the onset of shear banding occurs when the local shear rate exceeds a universal threshold. For complex WLM flows, this leads to the formation of a narrow high-shear band near no-slip boundaries, thereby creating effective slip in the remaining flow. We are preparing these results for publication and presentation at the Society of Rheology Annual Meeting.

We then turned our attention to understanding viscoelastic effects in bulk extensional flow of WLMs in the four-roll mill. WLMs exhibit a region of enhanced deformation rate near the stagnation point, which arises from significant strain softening of the fluid. This inhomogeneity of extension rate indicates that higher-resolution measurements are essential for better understanding of extension rheology of WLMs. Toward this end, we are in the process of developing a new flow cell based on the concept of a “microfluidic four-roll mill” with collaborators at NIST to enable such measurements using flow-small angle neutron scattering. To date, a device has been prototyped, and we are in the process of testing the extent to which it generates variable flow types.

In addition to these scientific impacts, PRF support has also greatly enhanced infrastructure of the PI’s lab, including a new rheo-PIV device (in concert with a generous donation from Unilever), computer codes for numerical simulations of viscoelastic wormlike micelle flows, and a new microfluidic four-roll mill device compatible with small angle neutron scattering measurements.

Detailed Progress

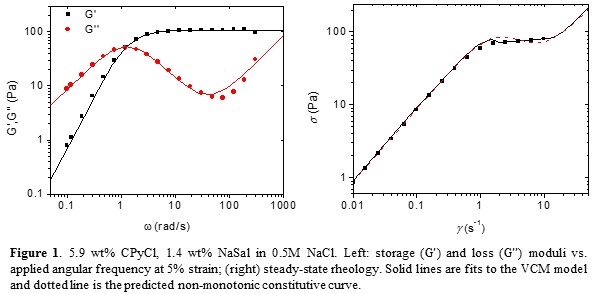
To study curvature effects on shear banding WLMs, we focused on a solution of 5.9 wt% cetylpyridinium chloride (CPyCl) and 1.4wt% sodium salicylate (NaSal) in 0.5M sodium chloride (NaCl).¹ The linear viscoelasticity is fit by the VCM model with a relaxation time of 0.78 s (Figure 1 left).^2,3 An apparent stress plateau occurs between 1 to 15 s^-1 under steady shear. These measurements were used to obtain best-fit parameters for the VCM model, which suggests a non-monotonic constitutive curve (right).^2,3

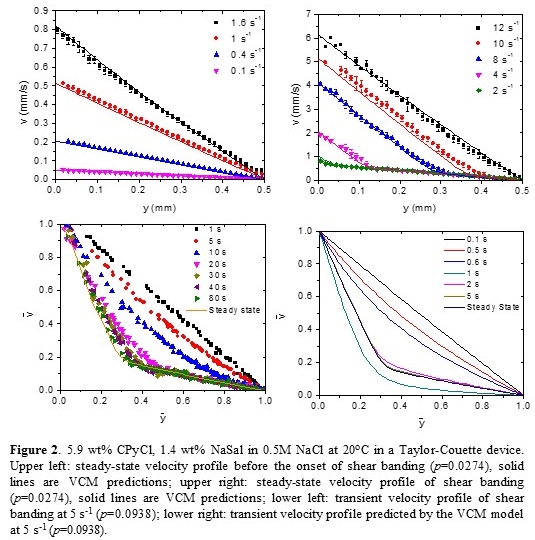
Rheo-PIV measurements in a Taylor-Couette device with systematically varying curvature, p (ratio of gap size to inner cylinder radius), are summarized in Figure 2. Before banding occurs, the velocity profile remains nearly linear (upper left). With increasing nominal shear rate, bands form and their interface migrates towards the static wall, while local shear rates in the bands remain almost constant (upper right). Although the VCM model agrees reasonably well with steady-state measurements, it fails to capture certain qualitative transient features, such as a slower time to reach steady-state and the absence of recoil during evolution of the velocity profile (lower left and right).

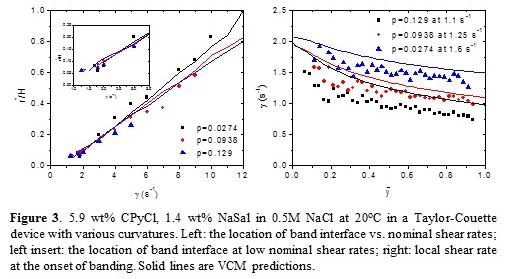
Increasing curvature (i.e., the inherent stress gradient over the gap) leads to an expansion of the envelope of critical shear rates for banding (Figure 3 left). The banding interface deviates significantly from the “lever rule” (linear dependence of the location of the interface between low and high-shear bands with shear rate) with increasing curvature, especially close to the critical shear rates (Figure 3 left). Interestingly, banding always begins after the local shear rate at the moving wall exceeds a critical value independent of curvature (Figure 3 right).

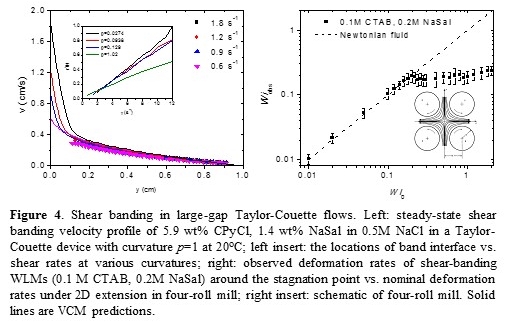
In complex flows, banding near surfaces has significant influence on the rest of the flow field. In a wide-gap Taylor-Couette device with p=1.02, a narrow high-shear band forms around the moving cylinder, and the surrounding velocity profile remains almost unchanged over a large range of nominal shear rates (Figure 4 left). Similar phenomena were observed close to individual rollers in a four-roll mill with “effective” curvature p=1.6. As a result, two-dimensional extensional flows on a shear-banding fluid within the four-roll mill exhibit nearly constant local dimensionless deformation rates, Wi_obs, with varying nominal deformation rate, Wi₀ for Wi₀>0.2 (Figure 4 right). Our studies indicate this is because the increased roller speed is effectively “absorbed” by the localized high-shear band.

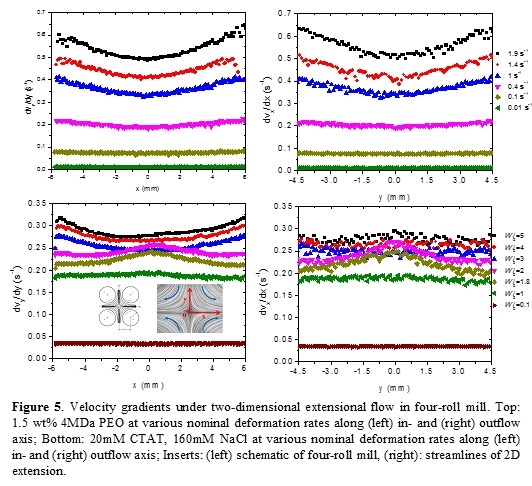
Finally, we studied viscoelastic effects (strain hardening/softening) on 2D extensional flows of shear thinning WLMs (20mM CTAT, 160mM NaCl) at high extension rates in the four-roll mill (Figure 5 top). 1.5 wt% ~4MDa polyethylene oxide (PEO) was used as a representative strain-hardening fluid for comparison. Above a critical threshold deformation rate, reduced extension rates are observed locally along the centerlines (y and x axis), attributed to strain hardening.⁴ By contrast, WLMs exhibit characteristics of strain softening (higher local extension rate along the centerlines) for intermediate extension rates, while strain hardening occurs along the inflow axis. Continuing studies are aimed at in situ stress/structure characterization and model calculations to better understand these observations.

1. Hu & Lips, J. Rheo. 2005, 49, 1001.

2. Vasquez et al., J. Non-Newtonian Fluid Mech. 2007, 144, 122.

3. Pipe et al., J. Rheol. 2010, 54, 881.

4. Zhou et al., J. Non-Newtonian Fluid Mech. 2014, 211, 70.

5. Dunlap & Leal, J. Non-Newtonian Fluid Mech. 1987, 23, 5.