59th Annual Report on Research 2014

This work focuses on depositional processes in buoyant, mud-rich river plumes in deltaic settings. The speed at which sediment is removed from such plumes is thought to scale with the settling velocity of the individual or flocculated particles in the plume. However, some studies suggest that vertical flux may not be so simple. Various instabilities can result at the density interface that lead to more complicated depositional processes that may be a function of more than individual particle sediment size. This work compares the vertical transport rate of flocculated mud settling as individual particles to vertical transport rates in stationary and moving stratified layers.

The experimental work for the project is being carried out in three phases. Phase 1 focuses on the development of an experimental sediment mixture, characterization of the flocculation behavior of the sediment, and measurement of the settling velocity of individual flocculated sediment. Phase 2 measures the settling rate and behavior of flocculated buoyant freshwater suspensions overlying clear saltwater in a stagnant stratification chamber. Phase 3 will then measure the settling rate and behavior of flocculated buoyant freshwater suspensions flowing out over a stagnant body of saltwater.

2. Progress

Phase 1

Completed last year.

Phase 2

Key items completed: Development of the experimental methods for Phase 2 was completed last year. During the 2013-2014 cycle, we finished all of the experiments, worked through the data analysis, and have drafted a manuscript on the combined results from phase 1 and 2. The paper will be submitted for review to Journal of Geophysical Research in October 2014.

Research Questions: The specific research questions examined with the phase 1 and 2 experiments are: (1) does flocculation hamper instability formation; (2) can individual floc settling adequately model removal rate of sediment from the buoyant layer; and (3), if not, is there a simple way to model the removal rate of sediment from the buoyant layer during sedimentation driven convection using information from the buoyant layer only?

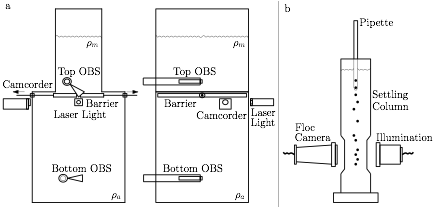
Methods: The two-layer system of a buoyant suspension of flocculated kaolinite clay overlying a base of clear saltwater was investigated in a laboratory tank. Concentration was continuously measured in both layers with a pair of OBS sensors, and the interface was monitored with a digital camera (figure 1). Snapshots from video were extracted to examine overall development of the instabilities at the interface and to measure finger velocity (figure 2). Samples of flocculated particles at the interface were extracted throughout the experiment to measure floc size using a floc camera (figure 1).

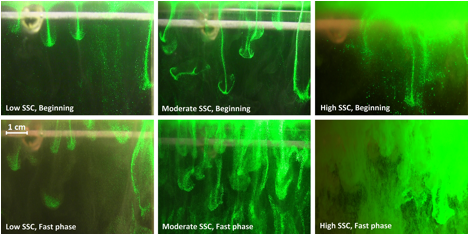
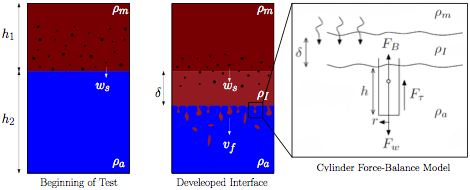
Findings: Results showed that the flocculation process did not stop the settling-driven convection even though large flocs were detected in many cases. In all cases, flocs settled through the initial fresh to saltwater interface to develop a so-called interface layer (figure 3). As sediment was added to this layer and the thickness grew, the layer became unstable and led to the development of convecting fingers at the bottom of the interface (figures 2 and 3). During the time of fingering, particle tracking near the interface showed that the vast majority of the sediment leaving the interface layer did so through fingers and not through individual particle settling. Descending particles near the interface would either get trapped at the interface (likely due in part to increased fluid motion in the region), or would be sucked into a finger to settle in mass.

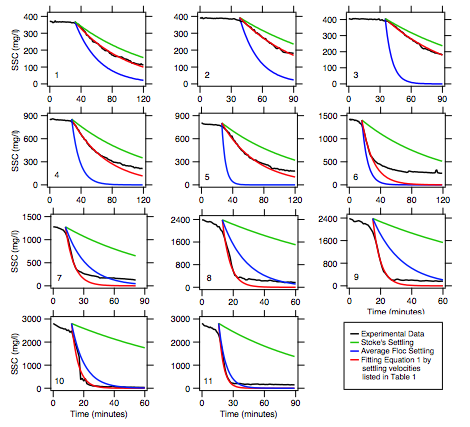
Comparison of the concentration time series in the upper layer showed that sediment removal did not scale with the Stoke's settling of the individual primary particles or the faster individual floc settling velocity. In some cases the true removal rate was higher than what was predicted with a simple settling mass flow rate of W_sCA. Other times it was higher (figure 4). It is reasoned that this occurs because removal during the time of fingering is more dependent on the finger velocity and total finger cross-sectional area than it is on individual particle settling. To model this, a simple cylinder-based force balance was used to develop an expression for finger velocity based on the suspended sediment concentration in the upper layer, and a critical Grashof number was employed to model the effective finger cross-sectional area also based on the concentration in the buoyant layer. Doing so allowed for modeling of the sediment flow rate leaving the upper layer as M = V_fA_fC where V_f = V_f(C) is the finger velocity and A_f = A_f(C) is the total finger cross-sectional area. The result is a mass removal rate due to fingers that is based solely on the concentration in the upper layer. The developed model works well as long as there is a density different between the interface layer and lower ambient. As time goes on, sediment added to the lower layer increases the density of the lower layer and sediment removed from the interface lowers the density of the interface. When the two densities are equal, the fingering process ceases and the simple model is no longer valid.

Figure 1. Sketch of general experimental setup

Figure 2. Sample images of convecting fingers for low, moderate, and high initial SSC

Figure 3. Overview of interface development and fingering and the terms in the force balance relation used to model the velocity of the fingers and mass removal rate from the interface layer.

Figure 4. Plots comparing the sediment removal rates predicted by individual particle settling (both Stoke's settling of primary particles and floc settling) with the experimental observations for each run.

Phase 3

Key items completed: We have tested a prototype experimental setup (figure 5).

Figure 5. Initial testing of stratified shear layer experiment.

Items still in progress: We still need to finalize the design of the experiment and collect and analyze the data. We have put this process on hold for the fall semester while we move universities. We plan to finish the remainder of the work at Virginia Tech during 2015 after the move has been completed. Academic year 2014-2015 is a no-cost extension year for the project.