59th Annual Report on Research 2014

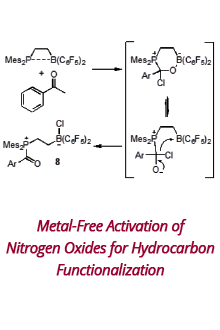
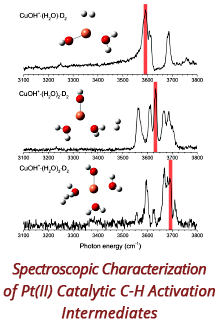
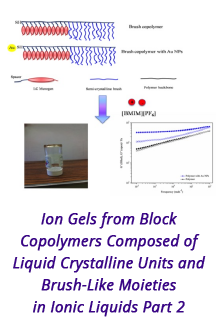
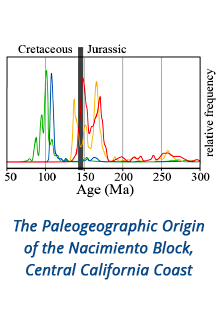
            This purpose of this research is to study non-Newtonian fluid dynamics, specifically of polymer and micelle solutions, in porous media with Pulsed gradient spin echo (PGSE) Magnetic Resonance (MR) techniques.  This work has relevance to enhanced oil recovery.  PGSE MR techniques have the ability to measure, non-invasively and without the use of a tracer, transport dynamics in opaque porous media.  Velocity images reveal the spatial distribution of velocity within the flow field, while probabilities of displacement measure anomalous diffusive dynamics as well as diffusion and dispersion in any direction.  To date, significant progress has been made and a publication is in preparation.  Figure 1 shows velocity images of water (figure 1a) and a micellar solution of 10 mM cetyl trimethylammonium p-toluene sulfonate (CTAT) in water (figure 1b) flowing in a model bead pack of 241 mm diameter polystyrene spheres. 

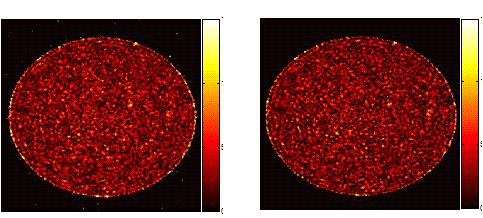
Figure 1.  Velocity images of water (left) and 10 mM CTAT in water (right) flowing through a packed bed of model spheres (d_p = 250 mm).  The spatial resolution is 55x55 mm over a 0.5 mm slice.  The colorbars correspond to a velocity range from black to red of 0-15 mm s^-1.

  CTAT is a shear-thickening wormlike micelle solution (figure 2).  The velocity fields for water and CTAT in Figure 1 appear very similar and exhibit the same statistics, i.e. average velocity and standard deviation.  This would indicate that the rheology of the CTAT solution does not impact the flow through the porous media.  

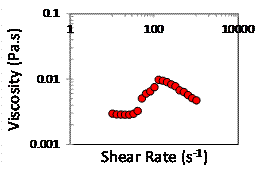
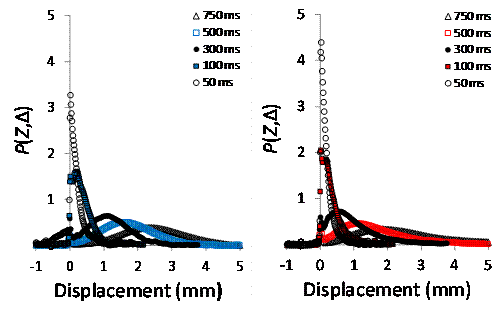
Figure 2.  Viscosity as a function of shear rate for 10 mM CTAT in water.

  However, measurements of the probability distribution of displacement, the propagator, reveal more complex dynamics.  For water (figure 3a) at short observation times (50 ms), displacements are centered about zero.  At long observation times (300 ms), the dynamics evolve to Gaussian statistics centered about an average displacement that depends upon the applied flow rate as expected.  In Figure 3b, however, the 10 mM CTAT solution exhibits non-Gaussian dynamics even at long observation times, including a peak at zero displacement and a long tail at higher displacements. 

Figure 3. Averaged propagators for a model porous media system (d_p= 241 mm, D= 6 mm). Water at 400ml/hr (left) and 10 mM CTAT at 400 ml/hr (right).  The Peclet number is 132.

  Figure 4a shows the propagators for the 750 ms observation time.  Water is largely Gaussian while the CTAT propagator is skewed towards lower velocities with a long displacement long tail.  Using a fractional dynamics approach with a Levy jump length distribution and plotting the propagators on a log scale (figure 4b), the slope of the curve at long displacement times reveals anomalous dynamics.  The long tail can be characterized as anomalous, or non-Gaussian, demonstrating that the shear-thickening material properties of the micellar solution impact the velocity field and hydrodynamic dispersion within a porous media.

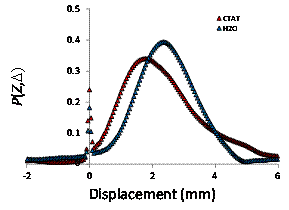
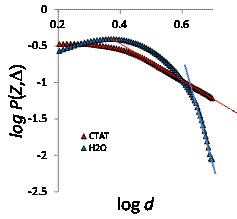
Figure 4.  At the left, averaged propagators at an observation time of 750 ms are shown for water (blue) and CTAT (red). At the right, the propagators plotted on a log-log scale.  At long displacement times, the slopes of the curves a correspond to Gaussian (a >2) and non-Gaussian statistics (a<2).

  This research has enabled the PI to fund a graduate student who will earn his MS in Chemical Engineering by December 2014.  This student has already obtained employment in the petroleum industry due to his research experience.  With this project, the PI has also obtained significant preliminary data suitable for application for ongoing funding to NSF.  The funding has had a high level of impact on the PI’s early career.