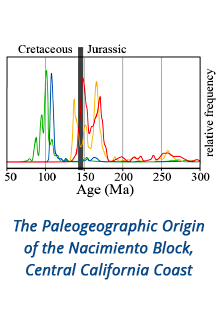
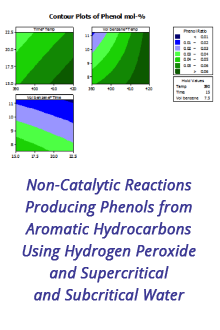
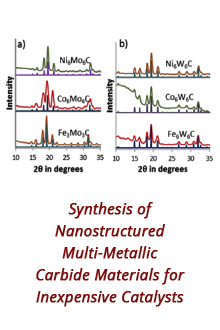
Reports: ND1053579-ND10: A Rheological Study of Interfacial Bacterial Films: Understanding the Mechanics of Two-Dimensional, Active Materials with Applications to Enhanced Oil Recovery
Robert L. Leheny, Johns Hopkins University
The experiments focus on a model system composed of aqueous suspensions of the bacteria Pseudomonas sp. in contact with hexadecane. By monitoring the mobility of colloidal spheres (radius, 0.5 micrometers) pinned to the oil-water interface, we investigate the evolution of the interface as the bacteria associate with it and form a biofilm. We find the interface undergoes a characteristic evolution over a timescale of hours that includes two distinct stages. In the first, the colloidal dynamics is dominated by swimming bacteria at the interface. This stage quickly gives way to a second stage in which the colloidal mobility becomes suppressed by the development of a viscoelastic film. Below, we describe the nature of the colloidal motion in each stage and its implications for film properties.
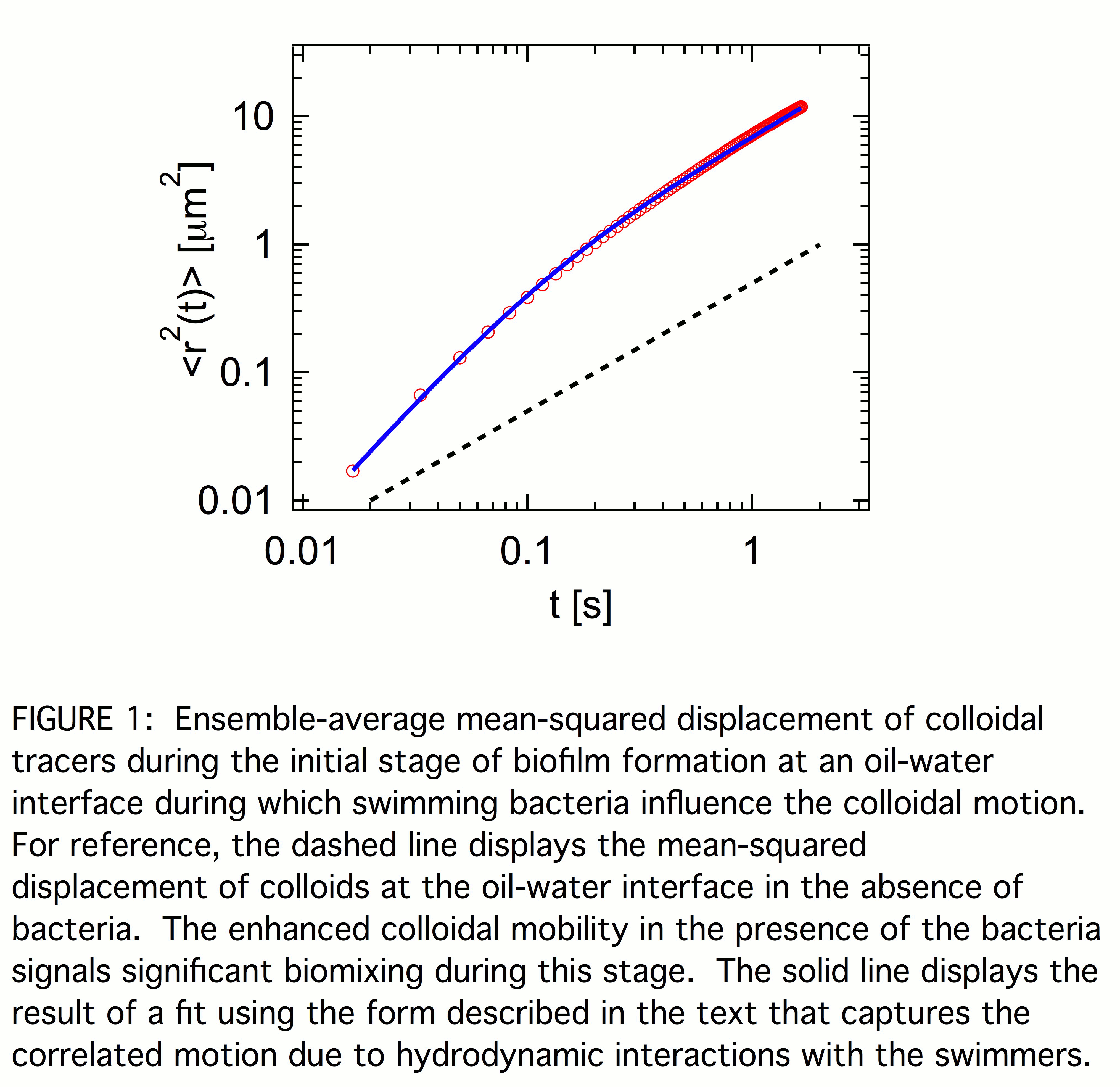
Figure 1 shows the ensemble-average mean-squared displacement <r2(t)> of the colloids during the first stage of biofilm formation in which the interface is populated with swimming bacteria. For reference, <r2(t)> of colloids at the oil interface of water containing no bacteria is also shown. In the absence of bacteria, <r2(t)> varies linearly with lag time t indicating simple diffusion, <r2(t)> =4D0t, with a diffusion coefficient, D0 = 0.12 µm2/s, consistent with the viscosities of water and hexadecane. The mean-squared displacement of the colloids at the active interface similarly varies linearly with t at large lag times, but with an enhanced effective diffusion coefficient. At smaller lag times, <r2(t)> grows more rapidly than linearly, indicating superdiffusive motion. Such superdiffusive motion signals temporal correlations in the forcing of the colloids due to hydrodynamic interactions with the swimmers. A simple model for these correlations ascribes to them a characteristic correlation time tau, so that the particle velocities have exponentially decaying memory. Such velocity correlations lead directly to a mean-squared displacement of the form <r2(t)> = 4D[t + tau*(exp(-t/tau) - 1)]. At short lag times, t << tau, this form predicts ballistic motion, <r2(t)> ~ t2, and at large lag times it reduces to diffusive motion, <r2(t)> =4Dt, with effective diffusion coefficient D. The solid line in Fig. 1 is the result of a fit using this form, which gives D =1.8 µm2/s. The value of D compared to that in the absence of bacteria, D/D0 = 15, indicates pronounced biomixing at the interface via the hydrodynamic flows created by the swimming bacteria. This biomixing likely has a strong influence on film formation. While the colloidal dynamics at large lag times with diffusivity D suggest the suspension of swimming bacteria act like a thermal bath with large effective temperature, the statistical properties of the colloidal displacements differ from those of a system in thermal equilibrium. Specifically, the probability distribution for particle displacements includes significant non-Gaussian components signalling enhanced probability of large displacements due to hydrodynamic encounters between the colloids and swimmers.
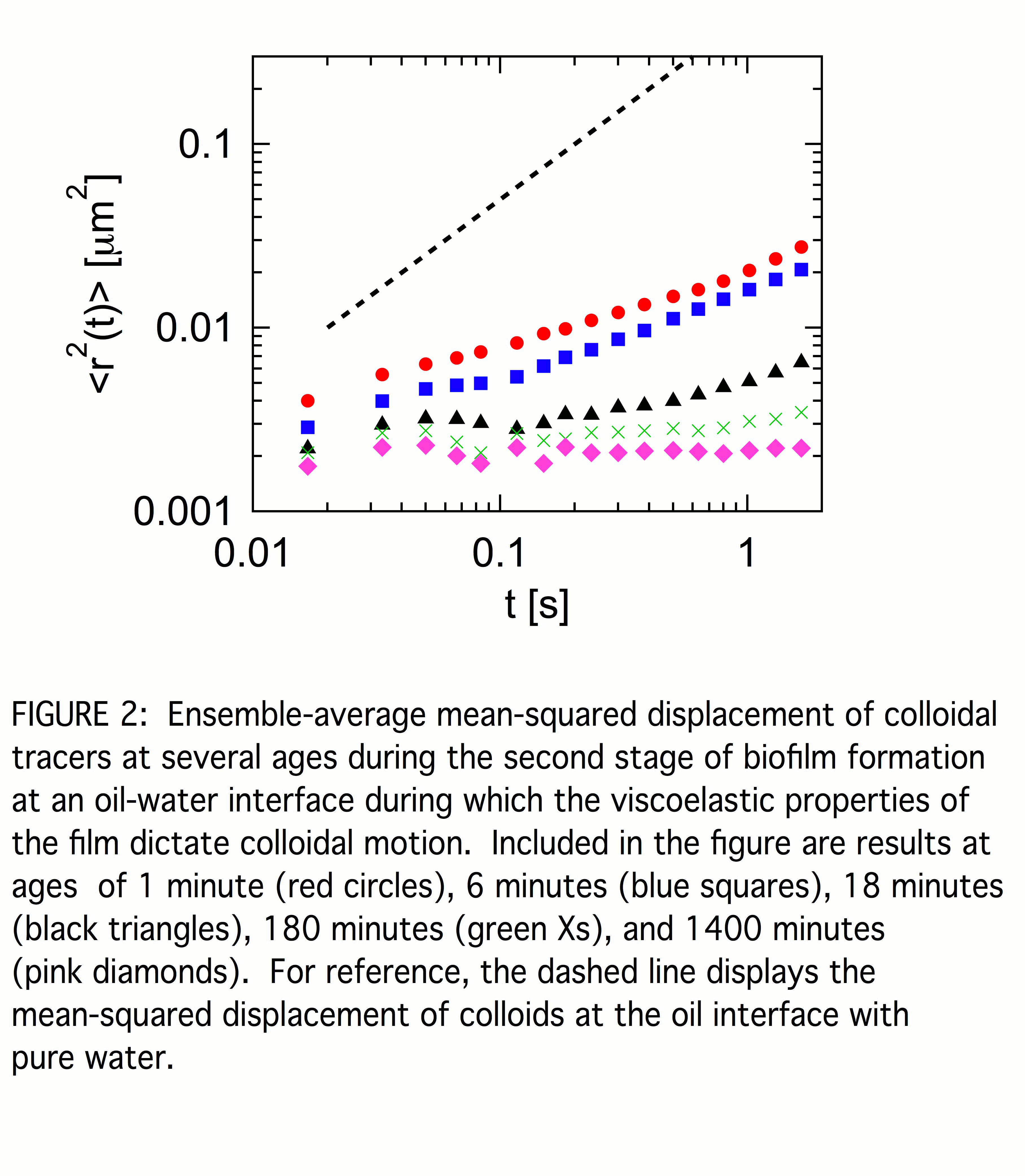
Typically, this initial stage of biofilm formation persists for less than five minutes, after which no motile bacteria are observed. We ascribe the limited duration of the bacteria motility to the lack of nutrient in the suspension. The end to the stage is reflected in a qualitative change to the probe dynamics in which <r2(t)> changes from superdiffusive to subdiffusive. Once the bacteria cease swimming, we treat the interface as a system close to thermodynamic equilibrium and consider the probes to be undergoing thermally-driven Brownian trajectories from which the film rheology can be inferred. Figure 2 shows <r2(t)> of the probes at several ages ta into this second stage. Again for reference, <r2(t)> of colloids diffusing at the oil interface of water containing no bacteria is also shown. Even at our earliest measurements in this stage, <r2(t)> is subdiffusive over the accessible range of lag times. Within this limited dynamic range, <r2(t)> is approximated as a power law, <r2(t)> ~ tn, with exponent n that is less than one and that decreases steadily with increasing age. Under appropriate conditions, one can obtain the frequency-dependent interfacial shear modulus, G*(f) = G'(f) + iG''(f), from <r2(t)> through a two-dimensional version of a generalized Stokes-Einstein relation. Specifically, a power-law <r2(t)> implies the film's shear modulus has power-law frequency dependence, G'(f) ~ G''(f) ~ fn. Such weak power-law frequency dependence of G*(f) is characteristic of the rheology of a range of disordered complex fluids and is indicative of a broad spectrum of relaxation times. The soft glassy rheology model, which provides a unifying theoretical framework for this behavior, explains this response as a general consequence of structural disorder and metastability. In this model, n serves as an effective noise temperature, with systems approaching a glass transition as n goes to zero. Thus, the steady decrease in n with layer age points to increasingly glassy dynamics characterizing the structural response of the biofilm.