59th Annual Report on Research 2014

Major goals of the project:

A broad range of industrially relevant fluids, including powders, suspensions, oil sands, and foams, exhibit shear banding: in flow, discontinuities in the velocity gradient develop, splitting the material into a high shear rate band and a low shear rate band.  The processing of shear banding materials is relevant to petroleum production from weakly consolidated reservoirs where shear bands play a critical role in wellbore collapse.

Recent theoretical and experimental work suggests that both interfacial and purely elastic instabilities may occur in these systems. Inertial instabilities are also likely, and these systems thus promise incredibly rich dynamics. In addition, optimal processing of shear banding materials requires an understanding of the scaling of instabilities with these driving forces (interfacial, elastic, and inertial), how these modes of instability interact, and how the boundary conditions affect stability. Wormlike micellar solutions provide a convenient and versatile model system for studies of shear banding systems, and are being used in the present study to gain a better understanding of flow transitions and instabilities in shear banding systems. 

We are using Taylor-Couette (TC) flow, that is, the flow between concentric, rotating cylinders, as the model flow for these experimental studies.  Using a custom-built Taylor-Couette apparatus, which allows independent, computer-controlled rotation of the two cylinders and the establishment of programmable ramping protocols, we are working towards (a) isolating purely elastic and interfacial transitions from inertial ones through the use of outer-cylinder rotation, (b) using counter-rotation of the cylinders to introduce a nodal surface and probe the effects of no-slip versus free boundary conditions for various instability modes, and (c) using a combination of counter-rotation, solution concentration, temperature, and inner cylinder radii to systematically explore the competition between interfacial, inertial, and elastic instabilities and understand how each mode scales with geometric (curvature) and kinematic variables.   

Ultimately, understanding the role of the destabilizing forces, the scaling of the instabilities with curvature, shear rate, normal stresses, etc., understanding the role of boundary conditions, and how the three modes of instability (interfacial, elastic, and inertial) interact, will improve the modeling of and impact processing of complex, shear banding materials. 

Accomplishments to date:   

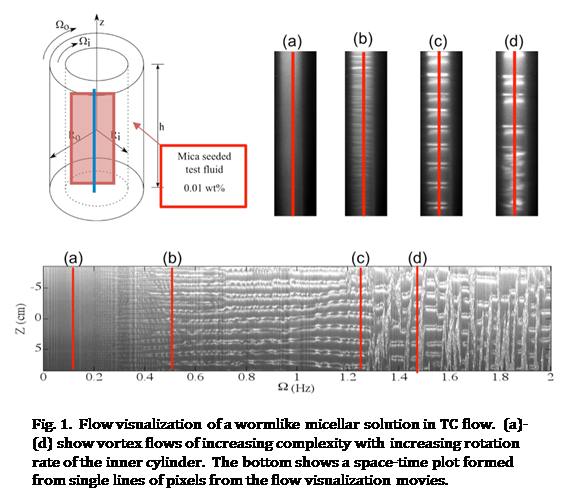
During this first reporting period, a postdoctoral scientist was recruited and trained in the operation of the Taylor-Couette cell and has been optimizing flow visualization, image processing, and spectral analysis methods. 

We have also performed linear and nonlinear rheological characterization on several candidate wormlike micelle solutions, and have begun performing Taylor-Couette experiments on an aqueous solution of cetyltrimethylammonium bromide (CTAB) with sodium nitrate (NaNO₃) similar to the one studied by Fardin and co-workers (Phys. Rev. Lett., 103, 028302, (2009)).   In our current experiments, the CTAB solution is seeded with anisotropic tracer particles, ambient lighting is used to illuminate the TC cell, and the z-q plane is imaged as the rotation speed W of the inner cylinder is slowly increased from zero while the outer cylinder is held stationary.  A series of flow transitions occurs, as shown in Figure 1 (top), where images 1a-1d show flow visualization images of the z-q plane as the purely azimuthal base flow (1a) is replaced by a series of vortex flows of varying wavenumber and complexity.  By taking a single line of pixels from each image captured and stacking them, a space-time (or, equivalently, z-W) plot is formed, as shown in figure 1(lower half). 

At present, we are working to understand the multiple time scales present in this system.  For example, by performing the experiment described above as a function of ramp speed of the inner cylinder, we can identify the sensitivity of the flow state to flow history for ramp rates above a threshold value.  Thus there is a time scale associated with this critical ramp rate.  Other time scales are those associated with shear band destabilization, formation of the interface, and the motion of the interface.  Understanding these various time scales is important to determining stability boundaries that are independent of flow history and can be faithfully reproduced in numerical simulations.