57th Annual Report on Research 2012 Under Sponsorship of the ACS Petroleum Research Fund

Primitive paths in "Olympic gels" deform affinely under moderate strains

We have applied our recently developed "isoconfigurational average" noninvasive method for observing the tube and primitive path in entangled polymers, to study "Olympic gels" under moderate extension and compression.  Olympic gels — melts of permanently linked long entangled rings — are a useful proxy for weakly crosslinked gels as well as long entangled melts at timescales short compared to the reptation time. 

We topologically equilibrate these systems in simulation, by occasionally allowing chains to cross, then turn off the crossings, and observe the chains fluctuating in their tubes.  We improve statistics by making many short movies from the same starting configuration, with different initial velocities (isoconfigurational average).  In this work, we progressively compress or extend melts of several long entangled rings to a total compression of 0.5, or total extension of 2.0, to see how the tube and primitive path respond under deformation.

Figure 1.  Representative primitive path after total strain 0.5, 0.66, 1 (undeformed), 1.5, 2.0 (blue); compared to affinely deformed primitive path at same strain (red).

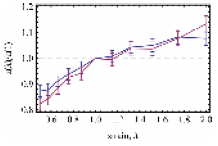
We find that for these modest strains, the primitive path deforms close to affinely (see figure 1 for representative example).  Likewise, the distribution of primitive path tangents (local directions of the tube) deforms nearly affinely as well (see figure 3).  The tube diameter, characterized by the width of the "cloud" of possible monomer positions around the primitive path, exhibits a modest dependence on strain (see figure 2).

Figure 2.  Tube diameter versus strain; blue and red results for different "movie lengths" (isoconfigurational averaging times).

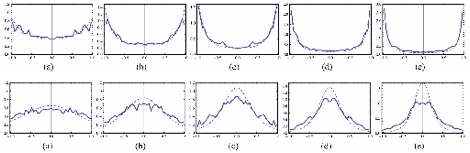
Figure 3.  Tube tangent distribution P(cos(θ)) for increasing extensional strain from 1.15 to 2.0 (top row), and for increasing compressional strain from 0.87 to 0.5 (bottom row), compared to affine prediction (dashed).

The strain dependence of the tube diameter in deformed gels is an important ingredient in theories of the nonlinear elastic response of these systems.  Our results provide a new, noninvasive, detailed look at the effect of modest deformations on the primitive path and tube.

Semiflexible primitive path suppresses early stress relaxation in entangled melts

We have recently applied our noninvasive methods for visualizing the primitive path and tube of entangled chains, to extensive united-atom MD simulation results of Mavrantzas et al. for entangled polyethylene melts (N=400 carbons), simulated for more than one reptation time.  In this case, we are not able to carry out isoconfigurational averages, but we can average over different portions of the full MD trajectory.

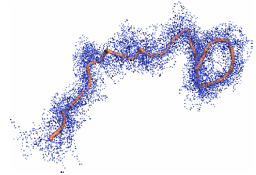
Figure 1.  "Cloud" of monomer positions (blue) and resulting primitive path (red).

One key result we obtain is that the primitive path for PE is semiflexible, just as for our earlier bead-spring simulations.  Likewise, the Kuhn length of the primitive path (about 60 monomers) is very close to the entanglement molecular weight for PE.  This makes sense because the primitive path can be thought of on a coarse-grained level as a freely jointed random walk of entanglement segments, with step length of the tube diameter.

Figure 2.  Equal-time tangent-tangent correlation function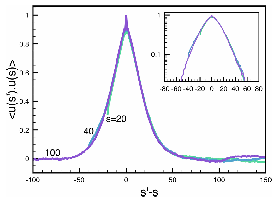
for the tube, versus arclength separation (different curves for different locations along the chain).

To investigate the dynamics of the PE chains simulated by Mavrantzas' group, we focused on what would be the "tube survival probability" for a simple reptation model, given by the following quantity:

This time-dependent correlation function is at the same time accessible in our primitive path analysis, and relevant to rheology.  We constructed an analytical theory based on contemporary rheological models, and found that these overpredict the "loss of memory" of the tangent near the ends of the chain.  (See figure 3.)  But when we modified the theory to account for the semiflexibility of the primitive path (as measured in figure 2), much better agreement resulted, without adjustable parameters.

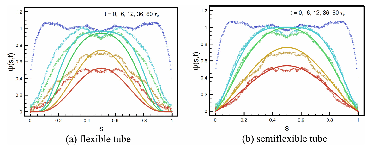
Figure 3.  a) tube "survival probability" from simulations (points) versus conventional tube-based theory (solid curves).  b) Improved agreement, accounting for primitive path stiffness.

Other authors have recently commented on the overestimate of stress relaxation near chain ends in conventional tube-based theories (with contour length fluctuations and constraint release).  Our results suggest that primitive path stiffness leads to tube tangents near the chain ends being longer-lived than expected, which preserves stress longer in that part of the tube.  This is an important modification for rheology of entangled short chains, and increases our confidence in tube-based theories.