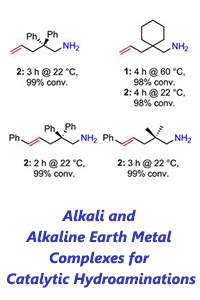
57th Annual Report on Research 2012 Under Sponsorship of the ACS Petroleum Research Fund

Polymer solutions are ubiquitously used in enhanced oil recovery (EOR) applications as viscosity modifiers for mobility control. The increased flow resistance offered by polymeric liquids, particularly in high permeability zones improves the reservoir sweeping efficiency resulting in enhanced oil recovery. In a water-wet rock surface, the oil droplets block pore openings and are difficult to dislodge because of interfacial forces. However, by introducing polymeric liquids that exhibit large flow resistance, the pressure drop due to the flowing polymeric liquid can overcome the Laplace pressure gradient associated with the oil droplet, resulting in the displacement of trapped oil. Thus, knowledge of the energy dissipation conferred by flowing polymeric liquids is a principal determinant of the efficacy of enhanced oil recovery applications.

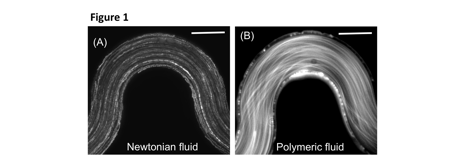
The flow resistance of polymeric liquids is often attributed to their high shear-viscosities. However, in complex geometries such as the reservoir porous media, the polymeric liquid flows through tortuous paths, and literature studies in model geometries have shown that the coupling of the curved streamlines and polymeric elastic stresses can create instabilities in fluid flow, even in the limit of zero Reynolds number (Re). For example, as shown in the curved channel fabricated in the PI's laboratory (see Figure 1), micron-sized beads mixed in a Newtonian fluid yield laminar flow streamlines, however the same beads dispersed in a polymeric fluid yield chaotic streamlines. Thus, it is possible that not only the high viscosity of polymeric liquids, but also purely elastic instabilities in curvilinear geometries could lead to enhanced flow resistance during polymer flooding operations in EOR applications. Despite recent advances in the understanding of elastic instabilities, knowledge of the frictional resistance induced by polymer instabilities in curvilinear channel (Dean) flows and its dependence on polymer parameters (molecular weight and concentration) is lacking. If this knowledge becomes available, then it could be used to predict the performance of polymers during polymer flooding operations. The framework being developed in this work could also be used to test newly designed 'green' polymers for their frictional resistance before field implementation.

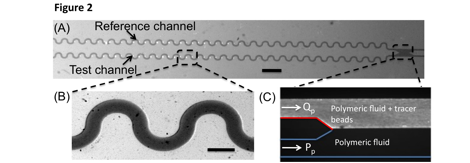
To quantify the contribution of polymer-induced elastic instabilities to the frictional resistance, we microfabricated a device containing serpentine microchannels as a model for porous media as shown in Fig. 2. To determine the mean flow resistance as well as fluctuations due to polymer-induced elastic instabilities requires instantaneous measurement of the pressure drop as a function of the flow rate in the microfabricated device. Conventional methods to measuring pressure drop, by attaching bulky pressure gauges are not ideal at the microscale, because of large dead volumes and compliance in tubing that could lead to long response times. Such non-idealities particularly complicate the quantification of fluctuations in flow resistance due to elastic instabilities.

We developed a novel 'comparator' tool that can perform in situ flow resistance measurement on the device, eliminating the need for external pressure sensors. The working principle of the measurement involves two identical channels – the test and reference channel – that are connected downstream to form a region where fluids can be compared (see Figure 2C). In a typical experiment, polymeric fluid seeded with tracer beads is introduced at a constant flow rate (Q_p) into the reference channel, and the same fluid is introduced at a constant pressure (P_p) into the test channel. The pressure is adjusted so that the fluids occupy almost equal width in the comparator channel, thereby 'balancing' the interface between the two fluid streams. Then the flow resistance is given by P_p/Q_p.

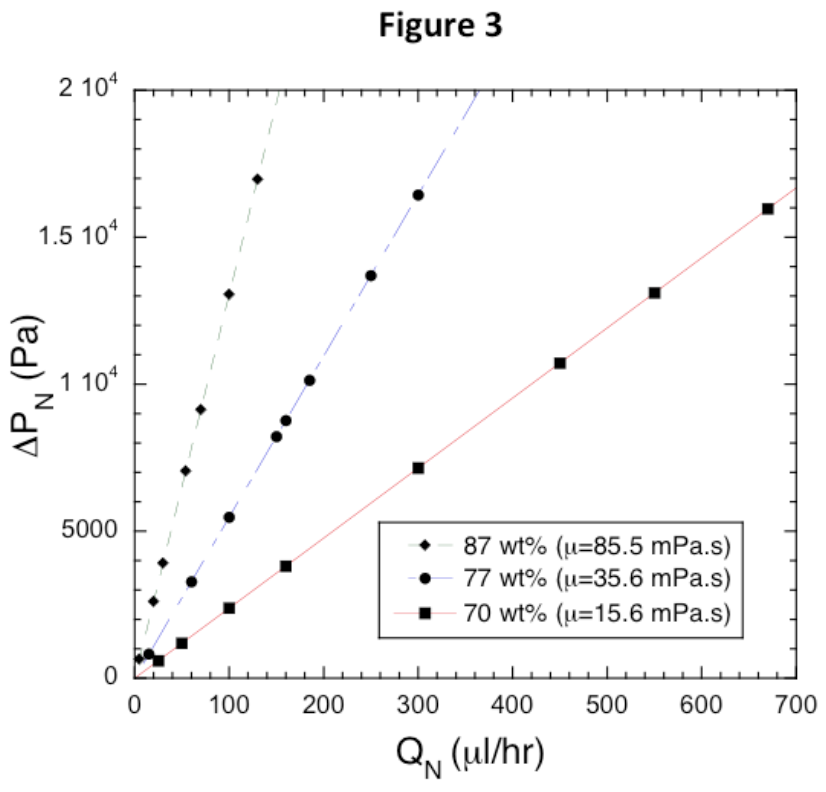
To test the flow resistance measurement technique, we introduced Newtonian fluids of know viscosity into each of our channels, and recorded the flow rate and pressure values needed to balance the interface. Fig. 3 shows the data obtained for fluids of three different viscosity. As expected the pressure drop increases linearly with flow rate for the three Newtonian fluids tested. The lines in Fig. 3 are the theoretical curves obtained by numerically solving the Navier Stokes equation for this geometry, with fluid viscosity and channel dimensions as the input parameters. Overall, the results in Fig. 3 indicate that the comparator tool can be used to measure the pressure drop due to flowing polymer fluids.

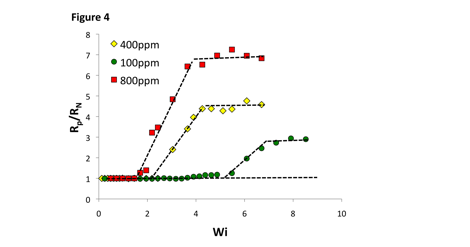
We next quantified the flow resistance ratio (R_p/R_N) due to the polymer-induced elastic instability as a function of Weissenberg number (Wi). Here R_p and R_N are the flow resistance due to the polymeric fluid and the same fluid without added polymer. Fig. 4 shows that for Wi < 1, the flow resistance ratio is close to 1, suggesting the lack of any instability. However, for Wi > 1, we observe an increase in the flow resistance, and finally at higher Wi the flow resistance ratio appears to saturate. Interestingly, we also find that as the polymer concentration is increased the flow resistance also increases.

Given that our tool is capable of sensitively measuring the flow resistance, the next steps in the project are to further explore the full dependence as a function of polymer molar mass and concentration, and establish empirical correlations of flow resistance due to polymer-induced elastic instability.

The ACS PRF Doctoral Investigator Grant had a significant impact on the PI's career. It led to a new area of research in the PIs laboratory, which otherwise would not have been pursued. The project is currently supporting a graduate student and has partially supported a postdoctoral researcher. Because of this award, the students have been trained in the several areas including microfabrication, fluid mechanics, polymer rheology and microscopy.