57th Annual Report on Research 2012 Under Sponsorship of the ACS Petroleum Research Fund
Reports: DNI250379-DNI2: Nanostructures Formation by Aromatic Hydrocarbons on Calcite
Chongzheng Na, PhD, University of Notre Dame
In the past
year, we focused on understanding the nature of the cation-p interaction between benzene (C6H6)
molecule and the calcite (CaCO3) surface. With the help of a
collaborator, quantum chemical calculations were performed for the benzene-calcite
interaction at the density functional theory (DFT) level. Using the program
package Gaussian, a benzene molecule was placed on top of the The energy of the cation-p interaction was estimated based on the formation energy of
calcite-benzene complex calculated from quantum chemical calculations, which
was E = 58.4 kJ mol-1. We further attempted to separate the
interaction energy into two contributions with one from the charge-quadrupole
electrostatic force and the other from the hydrogen bonding between the aryl
hydrogen atoms and the calcite oxygen atoms. The contribution from the
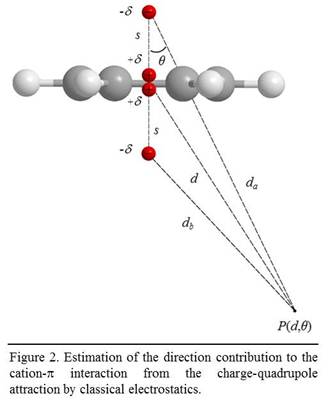
cation-π interaction is estimated using the classic quadruple-charge
interaction. As shown in Fig. 2, the potential field of the quadrupole is: where the quadruple moment Q = -2ds2,
ε0 = 8.85x10-12 C2 J-1
m-1, d is the distance from the testing point P to the
center of the aromatic ring, and q
is angle formed by the line connecting P and the ring center and the z
axis. This gives the energy of the cation-p
interaction to be: where q is the charge
of the surface calcium cation. Because each calcium ion has six bonds in
calcite, the nominal charge of surface cations is: where e = 1.6x10-19 C. Combining the above equations gives The values of Q for BTE molecules can be obtained
from the literature.
Recognizing d
is the distance from the center of the benzene ring to the calcium cation
underneath, we estimate the contribution from the charge-quadrupole
electrostatic force to be E1 = 18.2 kJ mol-1. The
contribution from hydrogen bonding was then computed as E2 = E
- E1 = 40.2 kJ mol-1. The calculation above
indicates that energetically, the cation-p
interaction between benzene and calcite is only 31% electrostatic but mainly
(i.e., 69%) due to hydrogen bonding. This insight regarding noncovalent cation-p interactions has not been reported
previously in the literature. We are currently verifying this finding by using
quantum mechanical methods to directly separate the contributions from the
charge-quadrupole electrostatics and the hydrogen bonding without the use of
classical approximation.
This grant has
made an important and positive impact on my career. It has provided me an
opportunity to pursue an idea that is deemed too risky for a junior faculty and
would otherwise have been shelved.
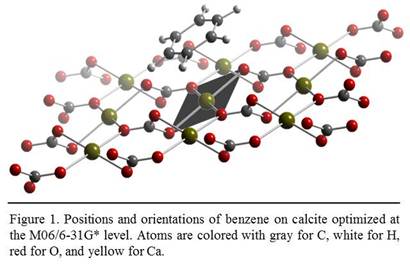
![]() cleavage
surface of a calcite slab consisting of 18 CaCO3 units. The position
and structure of the benzene molecule were optimized with the M06 functional
and a 6-31G* basis set. During optimization, the calcite surface was
structurally constrained. The result of the optimization was the structure of
the calcite-BTE complex associated with the global minimal total energy. As
shown in Fig. 1, after optimization the benzene molecule was arranged by the
cation-p interaction with its aromatic
ring facing the exposed surface calcium ions. Each surface calcium ions were
connected with 5 oxygen atoms from 4 surface carbonate ions and 1 carbonate ion
underneath; therefore, each of them had an empty orbital from the 4s3d5-hybridization
with a nominal charge of 1/3 of an elementary charge. The aromatic ring of the
benzene molecule was oriented most perpendicular to the surface so that the p electrons can enter the empty orbital of
the surface calcium atom. The aromatic ring was not centered over the calcium
atoms but rather shifted toward the recessed surface oxygen atom bonded to the
calcium atom.
cleavage
surface of a calcite slab consisting of 18 CaCO3 units. The position
and structure of the benzene molecule were optimized with the M06 functional
and a 6-31G* basis set. During optimization, the calcite surface was
structurally constrained. The result of the optimization was the structure of
the calcite-BTE complex associated with the global minimal total energy. As
shown in Fig. 1, after optimization the benzene molecule was arranged by the
cation-p interaction with its aromatic
ring facing the exposed surface calcium ions. Each surface calcium ions were
connected with 5 oxygen atoms from 4 surface carbonate ions and 1 carbonate ion
underneath; therefore, each of them had an empty orbital from the 4s3d5-hybridization
with a nominal charge of 1/3 of an elementary charge. The aromatic ring of the
benzene molecule was oriented most perpendicular to the surface so that the p electrons can enter the empty orbital of
the surface calcium atom. The aromatic ring was not centered over the calcium
atoms but rather shifted toward the recessed surface oxygen atom bonded to the
calcium atom.
![]()
![]()
![]()
![]() .
.