57th Annual Report on Research 2012 Under Sponsorship of the ACS Petroleum Research Fund

This report describes work in the past year to use a novel coarse-graining theory to develop new liquid state theories. Central is a theoretical framework developed in our group based on the relative entropy, a quantity that measures the information lost due to coarse-graining and that quantifies how well a putative coarse-grained system approximates one exhibiting more complex interactions. We previously demonstrated that minimization of the relative entropy offers a general and powerful strategy for designing accurate coarse models. Here, we pursued two lines of work in applying relative entropy coarse-graining to liquids.

Our first project aims to understand intrinsic scaling laws for liquid dynamic properties like diffusivity and viscosity. The past decades have showed that these are shaped and predicted by static structural and thermodynamic quantities, including on the basis of free volume and excess entropy theories. These ideas are suggestive that simple systems of particles with repulsive interactions are sufficient to predict kinetic properties in a wide range of more complex ones, provided the latter can be mapped appropriately. Indeed soft sphere models (particles with an inverse-power repulsion) can predict the density- and temperature-scaling of diffusion coefficients and relaxation times in simple liquids, mixtures, and polymers. For soft spheres, all state properties are a unique function of a single reduced thermodynamic variable ρ^m⁄3T^-1 where m is the repulsive exponent, and several groups have argued that effective soft sphere exponents can be be found for many systems that cast kinetic coefficients in this scaling.

Our work suggests that the repulsive perspective picture of dynamics can be generalized by a suitable mapping of arbitrary systems to reference soft-sphere models. We use relative entropy coarse-graining to convert reference simulations of a given system into a soft-sphere model. Importantly, we find many interesting relationships between the relative entropy and ideas from other theories of liquid state dynamics, namely those based on energy landscape theory, excess entropies, and energy-virial correlations. In particular, we show that the relative entropy approximately gives a Boltzmann-weighted but global measure of the differences in the soft-sphere and reference potential energy landscapes. We also show that it characterizes the associated excess entropy difference, and if diffusivities follow Rosenfeld scaling, the relative entropy then also measures the errors incurred in them due to coarse-graining. In that sense, minimization of the relative entropy should generate coarse liquid models that preserve not only thermodynamic by dynamic properties.

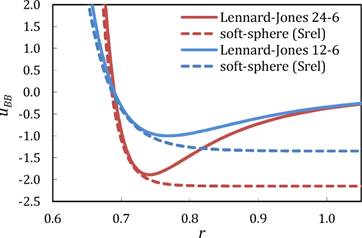
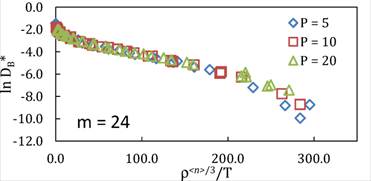
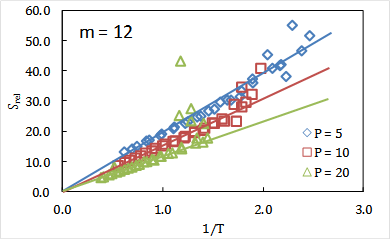
We tested this approach on well-studied models of binary glass-forming systems consisting of size-asymmetric particles interacting through Lennard-Jones-like potentials. Importantly, relative entropy minimization gives effective soft-sphere exponents that successfully collapse simulation diffusion coefficients according to soft-sphere scaling (Figs. 1-3). Moreover, the behavior of the relative entropy signifies that the soft-sphere landscapes become increasingly appropriate approximations at high temperatures and densities, as one might expect. These results are consistent with but formally distinct from earlier work on energy-virial correlations. We also find consistency between our calculations and excess entropy approaches to dynamics above the supercooled regime. This study suggests that the relative entropy may provide a flexible and integrated strategy for "perturbative" theories of dynamics, in which one can map any arbitrary system to a reference fluid model with simplified transport scaling laws.

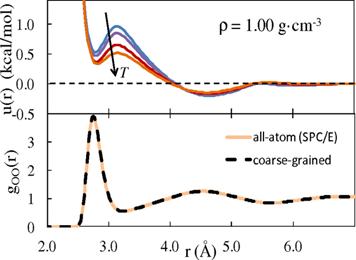
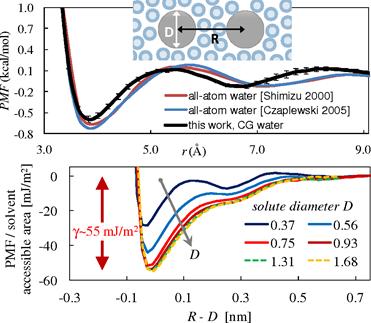
Our second project aims to develop a simplified picture of hydrophobic interactions (HIs), which are among the most important driving forces in colloid science, complex fluids, and biology. Many aspects of HIs remain unresolved; in particular, there has been a strong disconnect between simulations of weakly-associating small solutes and experimental measurements of strong forces between macroscopic surfaces. To explicitly address this scale-dependence of the HI, we used the relative entropy concept to develop a coarse-grained water model capable of simulating association free energies from small to macroscopic-sized solutes. In particular, we optimize an isotropic, "core-softened" potential that has been extensively studied as a "toy" model for waterlike fluids.

Our detailed simulations of solute association in this coarse water suggest a natural transition in the behavior of HIs with scale that provides a link between earlier simulations and experiments (Figs. 4-5). The simple water model captures small-methane association free energies known from expensive all-atom simulations; at the large scale, it correctly predicts the water-hydrocarbon surface tension and the experimental form of the distant-dependent attraction. Moving between these two regimes also shows the theoretically expected transition between entropically- and enthalpically-driven HIs, with a crossover near 0.7 nm that is consistent with earlier studies of solute hydration. The success of the model is explainable through simple geometric and integral equation arguments.

An implication of this work is the scale-dependent forms and driving forces for the distance-dependent "pure" HI. They provide a continuous picture for how the interaction evolves from the methane case to the macroscopic limit. We find that the HI is not merely a single force law, as its driving forces (entropy vs. enthalpy) and strength can be modulated through the sizes and separation distance of the associating groups. An equally important implication is that the HI might be understood in surprisingly simple terms, using an isotropic "core-softened" water model that balances two pair interaction length scales. These insights may lead to new numerical strategies in continuum solvation calculations.