57th Annual Report on Research 2012 Under Sponsorship of the ACS Petroleum Research Fund

During the initial eight months of the PRF project, the research was carried out by Daniel Smith, a graduate student currently in his second year, under the guidance of the PI. At this stage we have focused on two goals:

1.  to obtain high-level benchmark interaction energies for a class of model systems relevant for the methane (and other hydrocarbon) adsorption on graphene sheets and carbon nanotubes,

2.  to assess the accuracy of various novel density functional theory (DFT) variants relative to benchmark interaction energies and to select the approach(es) that provide the best performance.

The above goals have been fulfilled and the pertinent details are contained in a paper that will be submitted to the Journal of Chemical Theory and Computation within the next month. The research relevant to this project was also presented at four conferences.

1.  Accurate wavefunction-based benchmark interaction energies

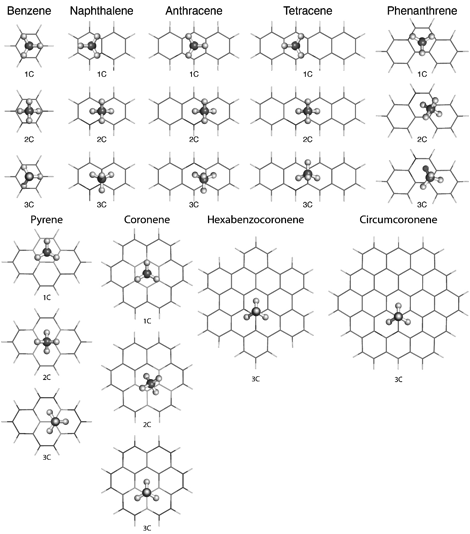
We selected a set of weakly interacting dimers of methane with polycyclic aromatic hydrocarbons (PAHs) benzene through coronene as model systems. For each dimer, we considered all three coordinations of the methane molecule, that is, geometries in which one (1C), two (2C), or three (3C) methane hydrogens are closer to the PAH plane than the methane carbon (Fig. 1). The lowest-energy structures for each coordination were identified via a MP2/aug-cc-pVTZ geometry optimization. Benchmark interaction energies were then computed for one-dimensional linear cuts passing through the optimized structures with a variable intermolecular distance.

Following the standard practice, benchmark interaction energies were calculated as  sums of the MP2 contribution extrapolated to the complete basis set (CBS) limit and the ΔCCSD(T) correction for effects beyond MP2 computed in moderate basis sets. The MP2/CBS values obtained in this work utilized the (aug-cc-pVTZ,aug-cc-pVQZ) and (aug-cc-pVQZ,aug-cc-pV5Z) extrapolations and are converged to within a few thousandths of a kcal/mol. Similar precision is not attainable for ΔCCSD(T). However, our extensive studies for benzene-methane and naphthalene-methane, involving basis sets up to aug-cc-pVQZ and the explicitly correlated CCSD(T)-F12 approach, indicate that the benchmark interaction energies are accurate to within 0.1 kcal/mol or better even for larger dimers where the ΔCCSD(T) term was computed in the aug-cc-pVDZ basis set (somewhat reduced for coronene-methane to avoid CCSD convergence problems).

Figure 1. Lowest-energy structures for the singly- (1C), doubly- (2C), and triply-coordinated (3C) methane-PAH complexes considered in the present work.

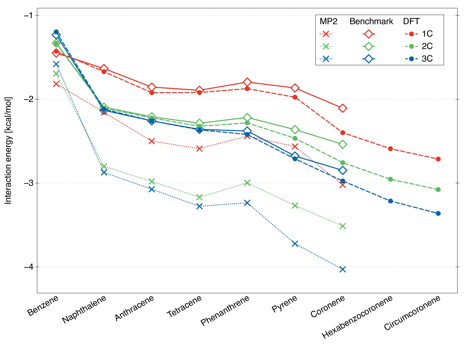
While the benzene-methane dimer has been extensively studied before, the interaction energies for larger complexes have not been previously obtained with any comparable accuracy. Our results indicate that the benzene-methane complex, with its 1C minimum structure, is an exception rather than a rule. For all larger dimers, the global minimum is triply coordinated and the 1C structure is the least bound of the three. The binding energies for all investigated dimers (Fig. 2) clearly show how MP2 recovers the general trends but overestimates the interaction energies by 30% or more.

Figure 2. Interaction energies for the lowest-energy 1C, 2C, and 3C structures of different methane-PAH dimers. The benchmark values are obtained as CBS-extrapolated MP2 energies augmented by the ΔCCSD(T) correction. The values marked as DFT denote the best performing B3LYP-D3/aug-cc-pVDZ functional.

2.  Selection of the optimal DFT variant

It is well documented that standard density functionals do not reliably treat the dispersion interaction, which is the main binding force between methane and finite or infinite carbon nanostructures. Therefore, one needs to resort to novel DFT approaches that have been formulated with weak interactions in mind. In this work we tested two classes of such approaches:

1. the DFT+D method using standard B3LYP, B97, and PBE functionals augmented by the –D2 and –D3 empirical dispersion expressions,

2. functionals that have been explicitly optimized for weak interaction energies: M05-2X, M06-2X, and ωB97X-D.

The above DFT variants were employed to compute methane-PAH interaction energies along the selected one-dimensional potential cuts. The resulting curves were compared to benchmark. The interaction-optimized functionals somewhat underperform for the systems considered – none of them gets below 10% in median relative accuracy. On the other hand, several DFT+D approaches are remarkably accurate as long as the counterpoise correction for basis set superposition error is included. The top performer, the B3LYP-D3/aug-cc-pVDZ method, leads to a median relative accuracy of 2.6% on all dimers from benzene-methane through pyrene-methane. Thus, B3LYP-D3 is the recommended DFT approach to study interactions between methane and extended carbon nanostructures.

3.  Towards extended systems – circumcoronene, graphene, and graphite

Equipped with a computationally efficient DFT approach validated against accurate benchmark data, we can set out to compute interaction energies between methane and larger PAHs all the way up to infinite systems. As the first step, we have calculated B3LYP-D3/aug-cc-pVDZ interaction energies for methane interacting with hexabenzocoronene and circumcoronene (Fig. 1). The results obtained for the latter system, corrected with the effects of distant carbon atoms in a graphene sheet, zero-point energy, and interactions with subsurface graphene layers, lead to an estimate of the methane adsorption energy on graphite equal to 3.58 kcal/mol (or 3.34 kcal/mol for the second best DFT variant, B97-D3/aug-cc-pVDZ), close to the experimental result but somewhat above its upper limit.

4.  Future work

The next step on the path towards accurate methane adsorption energies on carbon nanotubes is taking into account the nanotube curvature. This effect will be included by an appropriate extension of the coronene-methane and circumcoronene-methane models. In a parallel development, we plan on extending our DFT+D calculations to infinite systems using plane-wave basis sets and periodic boundary conditions. Finally, ensuring the proper behavior of dispersion for very large PAHs will probably require optimizing a completely new empirical dispersion expression. Work in these three directions is planned for the current year of the PRF grant.