57th Annual Report on Research 2012 Under Sponsorship of the ACS Petroleum Research Fund

Contributions. Dip-coating, in which a substrate is withdrawn from a bath, is perhaps the oldest and simplest form of liquid film deposition. The question posed in the original proposal was on resolving the long-standing controversy on surfactant effects in the classical dip-coating (Landau-Levich) problem [1], namely on the origin of the film thickening effect, which occurs in the presence of surfactants [2, 3]. An extensive body of experimental work has proven the validity of the analysis of Landau and Levich [1], who were the first to theoretically determine the thickness of the film deposited by the withdrawal of a flat substrate from a bath of liquid with a clean interface. However, there are a number of experimental investigations that have shown that surfactants in the liquid may result in a thickening of the deposited film. Marangoni phenomena have usually been considered responsible for this effect. However, some careful experiments [2] and numerical simulations [3] reported in the literature seemed to rule out this view as the cause of the observed behavior. Despite all these studies and the number of reports of film thickening, an experimental study of the flow field close to the coated substrate in the presence of surfactants has never been undertaken.

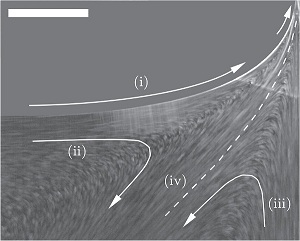
With the support of ACS PRF, we performed direct flow visualization of the Landau-Levich problem [4]. In this paper we presented a set of flow visualization experiments on coating of a planar substrate in the range of capillary numbers 10^-4 ≲ Ca ≲ 10^-3 for sodium dodecyl sulfate solutions with bulk concentrations of 0.25 CMC ≤ C ≤ 5.0 CMC. There are several important features of the flow field that merit description, as they are observed for each of the withdrawal speeds and surfactant concentrations tested. Although not distinguishable in a still image, analysis of the movies clearly demonstrates that the direction of motion of the interface at these scales is directed toward the substrate as indicated by (i) in figure 1(b). This is contrary to the clean interface case, cf. figure 1(a), where the direction of motion of the surface is away from the substrate and toward the bath as follows from the classical study of Landau and Levich [1] (in the film region, the free surface in the clean interface case moves upward at the substrate velocity).

Thus, the results presented in our work [4] suggest that the dip-coating with the soluble ionic surfactant SDS, under the conditions when the transport of surfactant is sorption limited and in the low capillary number regime, has the flow topology that can only be explained with a stagnation point residing in the bulk and not at the interface. As opposed to patterns with an interfacial stagnation point, the observed flow fields allow for the increase in film thickness due to the presence of surfactants compared to the clean interface case. Namely, such a flow field allows Marangoni stresses to be the mechanism responsible for the increase in film thickness over that predicted by the Landau-Levich law.

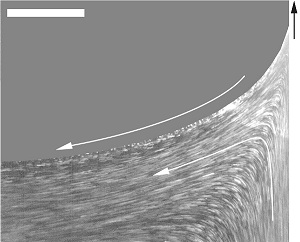
(a) c = 0.0. The small black arrow in the upper right hand corner indicates that the fluid near the substrate is carried into the film deposited on the moving substrate.

(b) c = 0.5. The small white arrow in the upper right hand corner indicates that fluid near the surface is swept into the film deposited on the moving substrate.

Figure 1: Flow field patterns in the clean 1(a) and surfactant-laden 1(b) interface cases. The velocity of withdrawal is U = 1.27cm∕s. Scale bar represents 2mm.

We also provided an explanation for the observed change in the steady-state flow topology from that in figure 1(a) to the one in figure 1(b). As in the case of any other bifurcation phenomena, it should happen due to the competition of physical effects (forces). First, the way the flow pattern in figure 1(a) is formed is as follows: (a) surface tension and gravity are responsible for the (static) shape of the interface; (b) viscous stresses due to moving substrate drag the fluid up, but because of the presence of the static interface, part of the dragged fluid is deflected into the bath thus leading to a stagnation point at the interface where the flow diverges into two parts going into the film and the bath, respectively. Second, once the interface becomes surfactant-laden, Marangoni stresses arise on both sides of the stagnation point. The latter disappears once the Marangonis stresses become strong enough and unidirectional. This happens when the Marangoni flow from the bath towards the film overcomes the counterflow into the bath, ‘breaks’ the separating streamline, and thus leads to the flow structure shown in figure 1(b).

Impact. At the educational level, the project allowed to train a graduate student and several undergraduate students (not directly supported by ACS PRF) in interdisciplinary research activities, as well as to enhance the education of other graduate and undergraduate students through results that are incorporated into courses taught by the PI. Active involvement of underrepresented groups in the research program at all levels was promoted through the NSF-supported California Alliance for Minority Participation at UCSB, through which the PI has already recruited a few students.

In conclusion, the proposed research provided fundamental proof-of-concept results, which will serve as a basis for an NSF proposal and place my group in a strategic position to continue research in a new to me field of physical chemistry. References