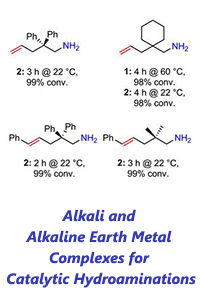
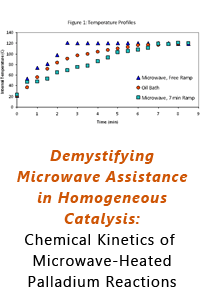
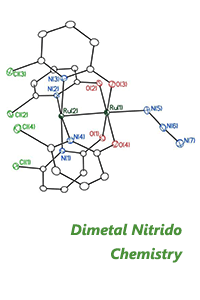
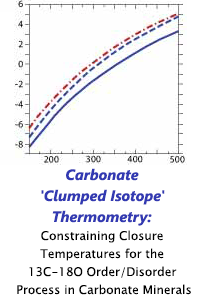
57th Annual Report on Research 2012 Under Sponsorship of the ACS Petroleum Research Fund
Reports: DNI851157-DNI8: Rock-Physics and Seismic Modeling of the Haynesville Shale
Kyle T. Spikes, PhD, University of Texas (Austin)
Overview and Goals
Modeling the elastic properties of the Haynesville Shale using rock-physics techniques is part of the characterization of this shale that could be used to improve predictions of economic drilling locations. The goal of this modeling is to relate the reservoir properties of interest (e.g., porosity, composition, and pore shape) to the elastic properties (P-wave and S-wave velocity). At the scales of available measurements, the Haynesville demonstrates horizontal layering and oriented inclusions that result in vertical transverse isotropy. Because of this observed symmetry, the modeling effort includes anisotropic analysis. Although the complex geometry of real grains and pores at the micro-scale control the elastic properties, we approximate those geometries with idealized grain and pore shapes within an effective medium model. More specifically, distributions of minerals, pore shapes, micro-cracks, and fluids are combined within a model to represent trends between the measured elastic and reservoir property data. Modeling of this type is based on well-log measurements, where the first priority is to identify which reservoir property or properties most significantly affects the elastic properties and explains general trends. Once this is determined, additional parameters are introduced to explain scatter that surrounds these general trends. Statistical treatment of all the reservoir properties provides distributions with which to assess ambiguity in the elastic response associated with combinations of shale properties. Ultimately, these distributions and the associated uncertainty will be related quantitatively to 3D seismic data to help to identify locations of economic drilling.
Results
Although the modeling is ongoing and evolving, the current status of this work is the implementation of two effective medium models to explain well log data from the Haynesville Shale. Those two effective medium models are the generalized self-consistent model (Berryman, 1995) and an anisotropic, pressure dependent model (Chapman, 2003). Estimates of composition of the Haynesville based on X-ray diffraction work from cores indicate a variety of minerals. To account for these possibilities, a large number of assemblages were considered, ranging from a majority of quartz and calcite with less clay, to assemblages with more clay and less quartz and calcite. Kerogen content was kept constant. Because these minerals naturally have different shapes and elastic moduli, we chose to model the solid component of the rock using the self-consistent model. It represent complex medium as a single homogeneous medium by including grains of different shapes and constituent moduli to determine the effective elastic moduli of the rock matrix. This matrix was then used as an input into the anisotropic model. Along with the matrix material, distributions of pores and micro-fractures were included. Ellipsoids were used to define the shapes of the pores and fractures, where the important parameter is the aspect ratio (the ratio of the short to long semi-axes). Inclusion shapes were correlated to composition. To link this to pore and micro-fracture shape, as the clay content increased, the pore and fracture aspect ratios were reduced. Results of this modeling approach provide vertical transversely isotropic elastic properties.
The most significant important result was the matching of both P-wave and S-wave data using this model. We did not see this result when trying to use various other effective medium models, some that were isotropic and some that were anisotropic. Because the model jointly explains P-wave and S-wave data, they can be used together to interpret the measured data in terms of the modeled reservoir properties. This interpretation is made in the sense of identifying combinations of the velocities that can be associated with reservoir properties most suitable for hydraulic fracturing and production. The overall effect of the anisotropic elastic modeling was reduction in the stiffness and rigidity of the effective medium due to both composition and to aligned, compliant pores and fractures. In terms of composition, some combinations of the velocities indicate large values of clay content. This situation suggests that although the rock could be fractured, the induced fractures likely would close relatively quickly due to the ductility of the clay minerals. Conversely, velocity combinations with more quartz and calcite are more brittle, and fractures likely would remain open for a longer duration. Because of the correlations between the composition and pore shape, compliant pore shapes correspond to relatively low velocities, and these flat pores would tend to close more quickly after production. This rock physics model suggests that locations in the Haynesville Shale with low P- and S-wave velocity indicate more clay content and flat, elongated pores. Combinations of faster velocity potentially may be more suitable for fractures to remain open for longer time periods.
Future work
Constructing various geologic scenarios indicated if significant changes in the seismic velocities occur due to a change in rock properties. The modeling up to this point indeed identifies such scenarios. However, the combinations of velocities discussed are inherently uncertain because multiple combinations of rock properties have similar or identical seismic velocities. Thus, the next step is to assess this uncertainty by examining errors in the measurements, errors in the model itself, and errors in the match between the model and the data.
Application of the modeling results to 3D seismic data is the ultimate goal of this project. This will include understanding how the trends identified at the well log scale behave at the larger seismic scale where resolution is much lower than for well data. The anticipated way forward is to generate earth models similar to the modeling method presented here. Those earth models will be converted to elastic properties, from which full-waveform synthetic seismic data will be computed. Full-waveform seismic data will be needed to account for the anisotropy. Those synthetic seismic signatures will then be analyzed in terms of trends and uncertainty analysis.
Berryman, J. G., 1995, Mixture theories for rocks. In Rock Physics and Phase Relations: a Handbook of Physical Constants, ed. T. J. Ahrens. Washington, DC: American Geophysical Union.
Chapman, M., 2003, Frequency-dependent anisotropy due to meso-scale fractures in the presence of equant porosity: Geophysical Prospecting, 51, 369-379.