AmericanChemicalSociety.com

Ground-penetrating radar (GPR) is an excellent method to image shallow sedimentary structures because the signal response is controlled by textural properties. GPR has traditionally been used for 2D and pseudo-3D characterization, but recent studies have demonstrated the added value of full-resolution data, with less than quarter wavelength sampling for in- and cross-line directions. The objective of this project has been to characterize and quantify 3D internal structures for various depositional settings through a combination of full-resolution GPR imaging and statistical analysis of facies and reservoir properties.

Reconnaissance GPR data have been collected for a range of sedimentary deposits, including marine, coastal, fluvial, eolian, and glacial (Table 1). In the Great Lakes region, data were collected at a beach ridge along Lake Erie, a wind-blown dune system along Lake Michigan, an esker deposit in central Michigan, and the point bar of a meandering creek in west Michigan. Full-resolution 3D GPR data were collected to test experimental procedures at an archeological site and in a fractured limestone quarry. The majority of research in this project, however, has focused on a number of full-resolution 3D data cubes that were collected at a site with heterogeneous fluvial deposits in Mississippi.

At this site on Columbus Air Force Base (CAFB), Mississippi, we collected non-aliased 3D GPR data (less than ¼ wavelength in- and cross-line spacing) using both 50 and 100 MHz antennas. The step size was set at 0.2 and 0.1 m for the 50 and 100 MHz antennas, respectively. Data were collected using a sampling interval of 800 ps over 550 and 400 ns time windows, and 16 and 32 stacks for the two frequencies, respectively. Data collection was triggered by an odometer, with positioning controlled by guidance ropes; the position error due to wheel slip was on average less than 1%. GPR data were processed with a background removal filter (dewow, 14 and 8 ns for 50 and 100 MHz, respectively) followed by a band-pass filter to eliminate high-frequency noise. Static corrections were then applied to flatten the reflection from the top of the saturated zone. The reflection times for the saturated zone were converted to depths based on the average measured velocity of 0.058 m/ns, from CMP and cross-borehole data.

Our research benefited from past and ongoing research at this site that focuses on contaminant flow in heterogeneous aquifers. Corroborating information includes various detailed grain-size cores and high-resolution information on hydraulic conductivity based on flow meter and direct push measurements.

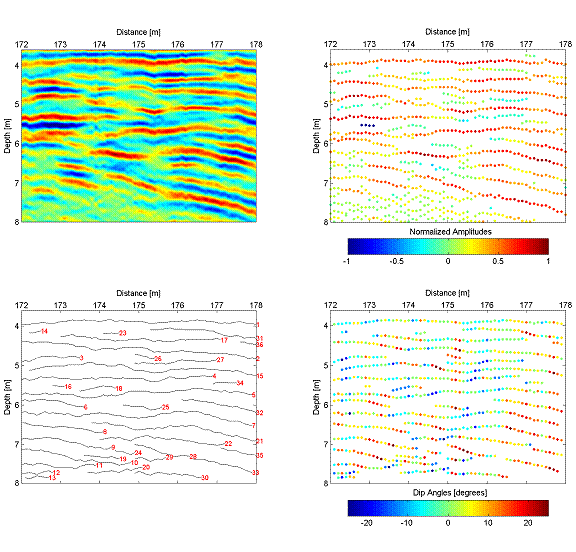
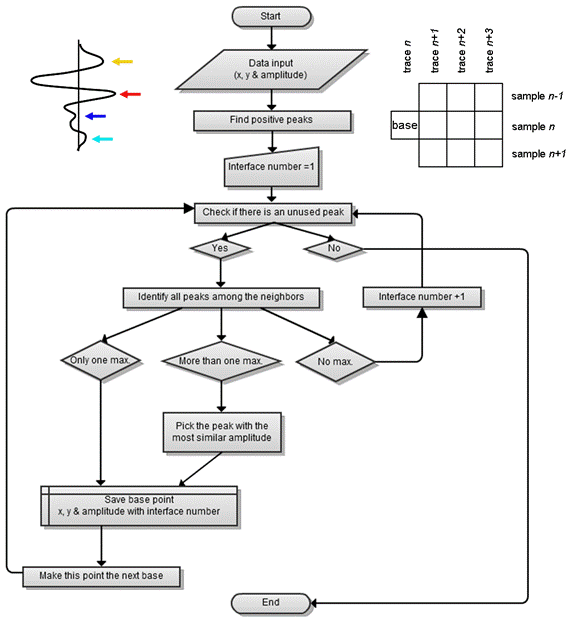
To facilitate automatic analysis of the large volumes of data we developed a Matlab algorithm that picks reflections and identifies these as individual interfaces through information on lateral continuity and dip. A flowchart of the procedure is given in Figure 1. First, all peaks in the data are identified. In the example (Fig. 1, top left), all positive peaks, irrespective of amplitudes, were selected. Starting with an arbitrary peak in the dataset (in the example the top left of the plane), the algorithm will identify all amplitude peaks among its neighboring points (Fig. 1, top right). The size of the neighbor grid can be varied depending signal and sampling characteristics; neighbor weights can be varied if necessary. If no peak can be found among the neighbors of a base point, a new interface/layer is started. Figure 2 shows the results of the algorithm using an example 2D section of data from CAFB. After indentifying the peaks in the data (Fig. 2, top right), the algorithm identified a series of continuous reflections that can be analyzed quantitatively (e.g., dip angle).

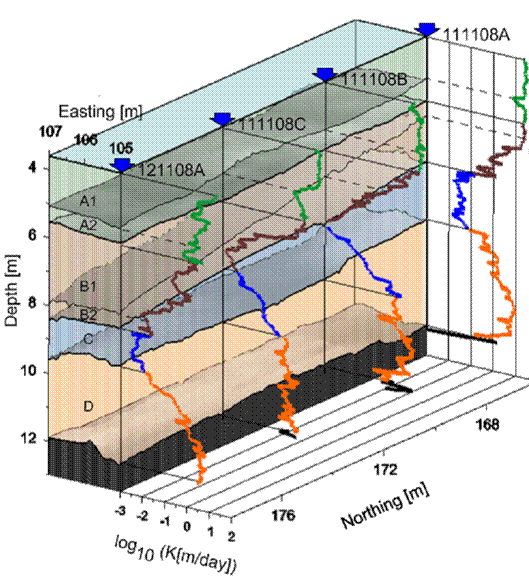
Our research focused in part on the question whether it is possible to populate identified GPR facies with aquifer properties in three dimensions, as such realizations would greatly benefit modeling of flow and transport through heterogeneous aquifers. For one of the 3D cubes collected at CAFB, a GPR facies approach was used to separate the data into four main units (Fig. 3). Qualitative comparison with four collocated hydraulic conductivity profiles suggests that both methods can be used in tandem for true hydrostratigraphic analysis. A paper that was recently published in Geophysical Research Letters (Dogan et al., 2011) evaluates this possibility quantitatively. In this paper, we demonstrate through statistical analysis of hydraulic conductivity values within GPR facies, sub-facies, and layers that 3D subsurface structures can be reconstructed with their correct geometries and hydrologic attributes.

Table 1. GPR data were collected using PulseEkko (PE) equipment from Sensors and Software ProEx equipment from MALA Geoscience, with frequencies ranging from 50 to 500 MHz depending on the depth of interest and the required detail.

Figure 1. Flow diagram for Matlab algorithm used to convert GPR data into a line plot with laterally continuous reflections.

Figure 2. Results of the Matlab algorithm for sample 2D dataset collected at CAFB.

Figure 3. 3D GPR facies boundaries (shaded to visualize topography) with four collocated profiles of high-resolution hydraulic conductivity. The hydraulic conductivity profiles were collected by colleagues from the Kansas Geological Survey. From Dogan et al. (2011).