AmericanChemicalSociety.com

Hypsometry of submarine canyons and gullies in the central US Atlantic slope

Dina Vachtman, Neil C. Mitchell

The University of Manchester, Faculty of Engineering and Physical Sciences, School of Earth, Atmospheric and Environmental Sciences, Manchester, United Kingdom

Submarine valley systems of the central Atlantic USA slope (Fig. 1) have a number of remarkable similarities with bedrock-eroding fluvial valley systems, in both a visual (qualitative) and quantitative geomorphic sense (e.g. Twichell and Roberts, 1982; Schlee and Robb, 1991; Mitchell, 2004). 

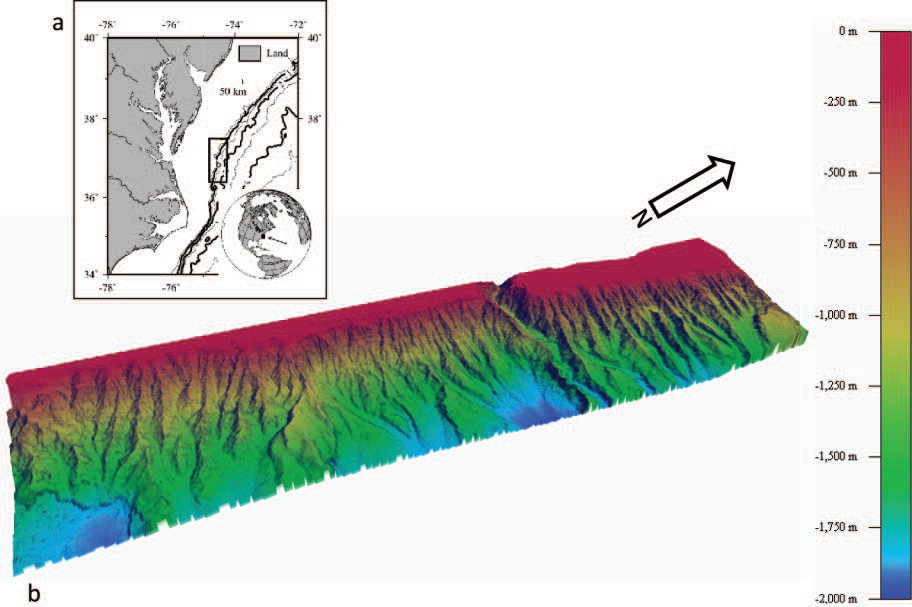
Fig. 1. (a) Location of the multibeam echo-sounder data (adapted from Mitchell, 2004) and (b) Colour-relief image of bathymetry of the USA Atlantic continental slope off Virginia. The data were collected with multibeam echo-sounders of National Ocean Service survey ships Whiting and Mt Mitchell and made available by the National Geophysical Data Centre (Coastal Relief Model).

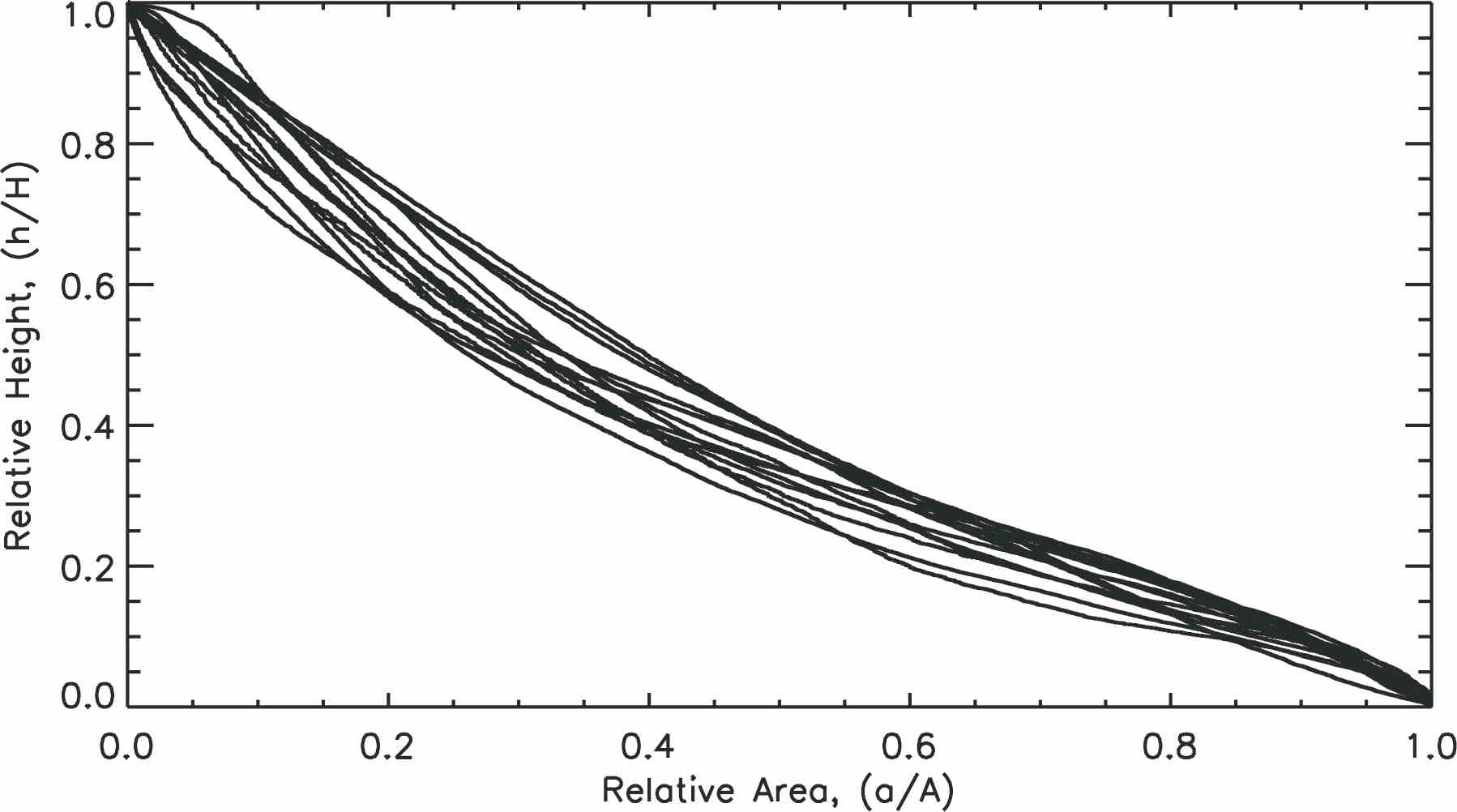
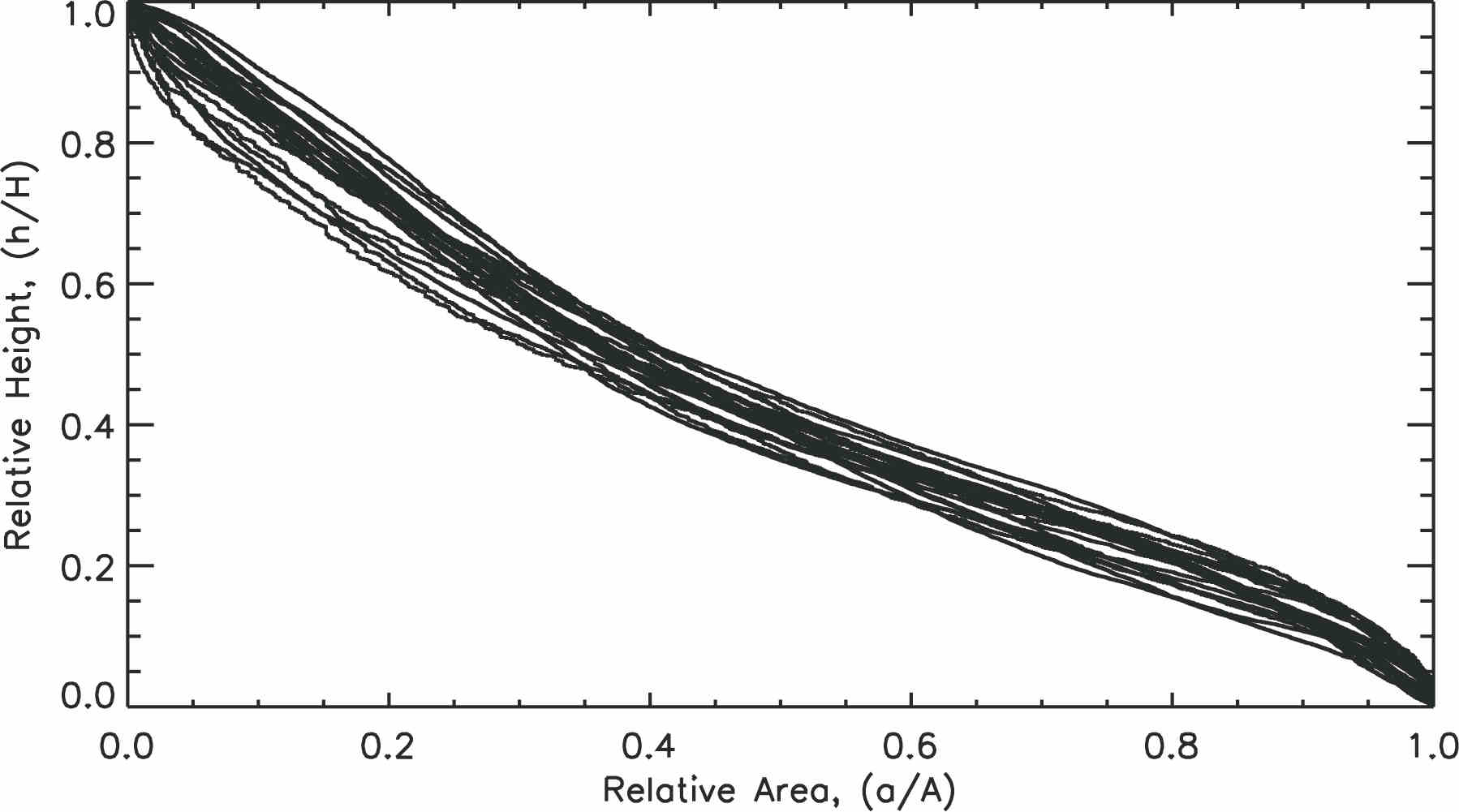
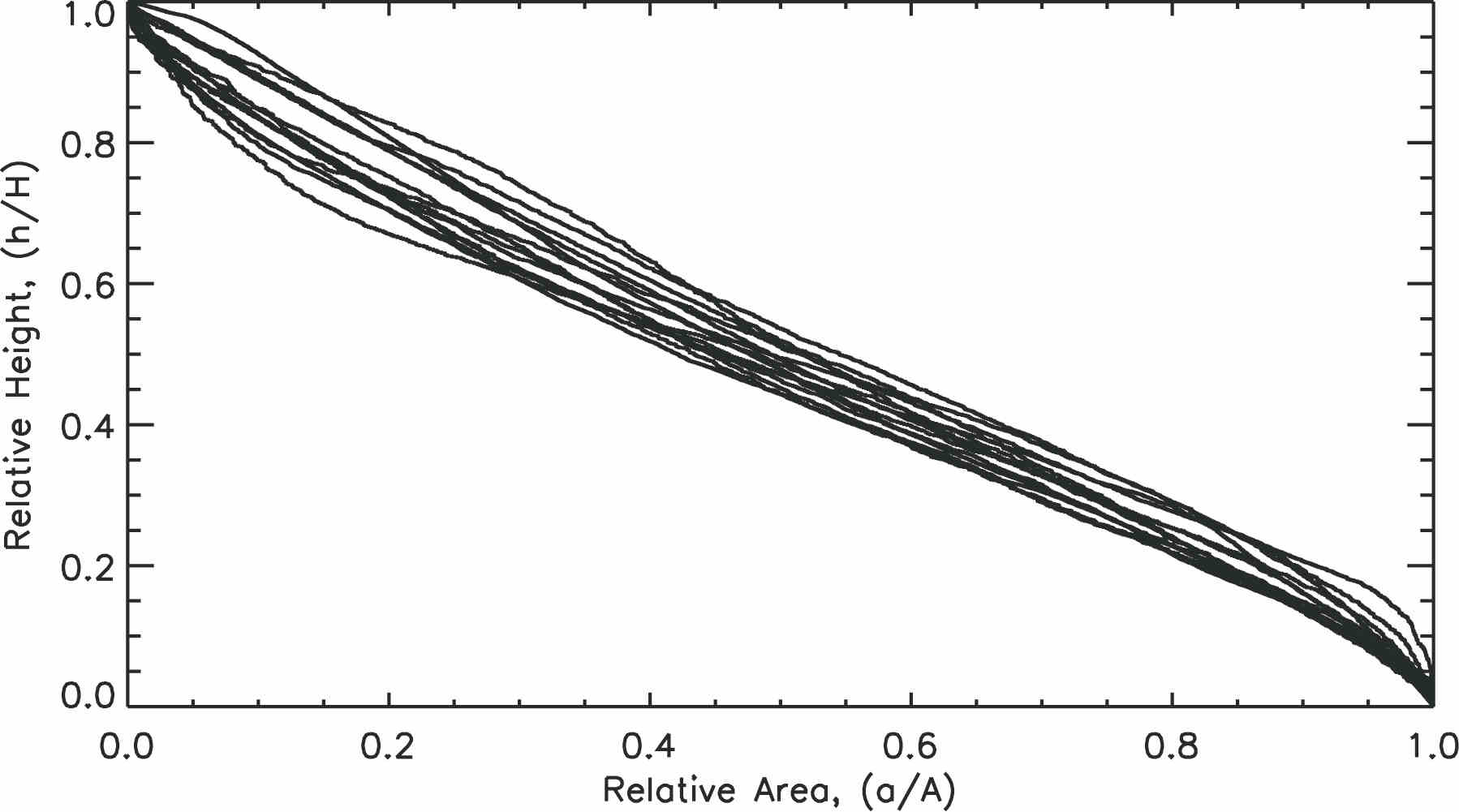
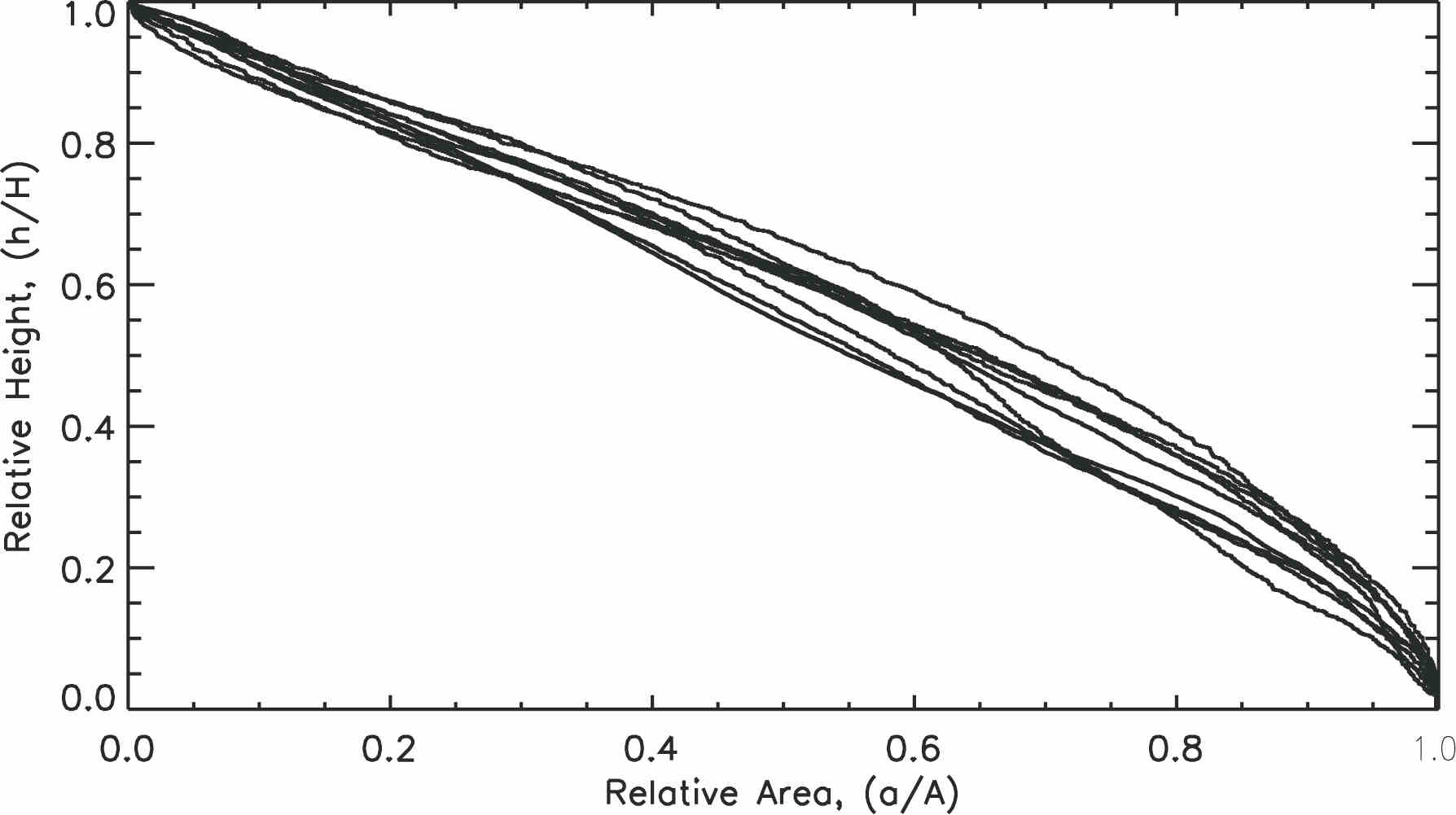
The origin of these submarine slope valleys has been controversial, with some arguing that top-down fluvial-like erosion by turbidity currents has dominated (e.g. Stanley et al, 1986), while others have argued that they were created by retrogressive failure initiated in the lower slope (e.g. Farre et al, 1983), or a hybrid of the two (Pratson and Coakley, 1996). No comprehensive scheme yet exists to relate the submarine landscape morphologies to formation processes. As a step towards that goal, we employed hypsometry (area-elevation analysis) to characterize the large-scale geomorphology of the canyons so that comparisons can be made between them and with similar features in subaerial landscapes. Hypsometry is a method used to characterise the distribution of area with elevation in a landscape. We have derived such curves for the USA Atlantic slope canyons. Treating the curves as cumulative probability distributions, we have calculated simple statistical parameters (skewness, kurtosis and integral) which are useful for discriminating relatively small differences in curve shape. The skewness in particular was found to discriminate four different hypsometric curves types: toeless concave, S-shaped, flattened-J-shaped and convex (Fig. 2).

2A. Type I- toeless concave

2B. Type II- S-shaped

2C. Type III- J-shaped

2D. Type IV- Convex

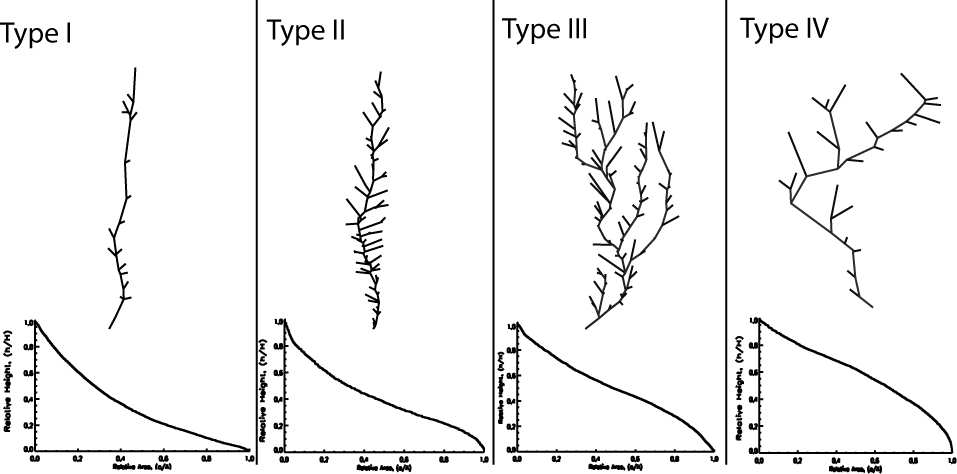
Figure 2. Four types of hypsometric curves as classified using their statistical attributes. If we attempt to interpret these in terms of classical ideas of eroding landscapes used in subaerial settings, the following might be inferred. 2A. Type I- toeless concave: the curves are concave in the middle portions, compatible with more erosion in the central reaches of the networks. 2B. Type II- S-shaped: the curves are concave mostly in the middle, again compatible with more erosion along central reaches. 2C. Type III- J-shaped: the curves are convex in the middle to lower portions of the network, compatible with most erosion in the upper reaches of the networsk and less erosion in the lower reaches. 2D. Type IV- convex: the curve is more convex in the middle to lower portion, compatible with more erosion in the upper reaches of the networks.

The curves have turned out to correspond remarkably well to network geometries in plan view. Narrow networks and straight trellis patterns correspond with toeless concave and S-shaped hypsometric curves. A decrease in the aspect ratio and more highly branched networks correspond with flattened-J-shaped and convex curves (Fig. 3). We are now developing further observations to see whether they might indicate how submarine processes acting along the US Atlantic slope affect these tendencies.

Fig. 3. Correspondence between plan-view of the networks and hypsometric curve types. Type I- linear canyons with poorly developed trellis network have toeless concave hypsometric curves; Type II- canyons with well developed trellis network have S-shaped hypsometric curves; Type III- canyons with dendritic tributary networks have J-shaped hypsometric curves; Type IV- Upslope dendritic canyon systems with low drainage-densities have convex hypsometric curves.

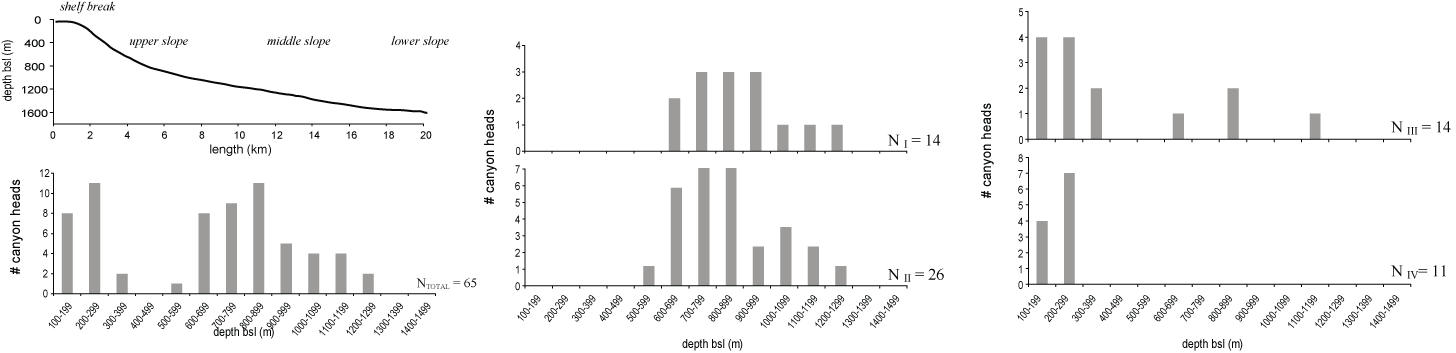
Figure 4. (a) Representative slope profile for the study area and (b) distribution of total number of network heads (N=65) with depth (bsl) and each of type (c) Type I, (N=14), (d) Type II (N=26); (c) Type III (N=14) and (d) Type IV (N=11). The more linear canyons (types I and II) are slope-confined whereas the more dendritic (types III and IV) can intersect the shelf edge in places.

The statistical characteristics of these hypsometric curves provide simple parameters that allow us to map out canyon geometry represented by them to compare with possible controlling varied factors.

References:

Farre, J.A., McGregor, B.A., Ryan, W.B.F. and Robb, J.M., 1983. Breaching the shelfbreak: passage from youthful to mature phase in submarine canyon evolution. In: D.J. Stanley and G.T. Moore (Editors), The shelfbreak: Critical interface on continental margins. Society of Economic Paleontologists and Mineralogists Spec. Publ. 33, pp. 25-39.

Mitchell, N. C. 2004. Form of submarine erosion from confluences in Atlantic USA continental slope canyons. American Journal of Science, 304, 590–611.

Pratson L.F., and Coakley, B.J., 1996, A model for the headward erosion of submarine canyons induced by downslope-eroding sediment flows, Geological Society of America Bulletin 108 (2), pp. 225–234.

Schlee, J.S. and Robb, J.M., 1991, Submarine processes of the middle Atlantic continental rise based on GLORIA imagery: Geological Society of America Bulletin, v. 103, p. 1090-1103.

Stanley, D.J., Culver S.J. and Stubblefield, W.L., 1986, Petrologic and foraminiferal evidence for active downslope transport in the Wilmington Canyon. Mar. Geol. 69, pp. 207–218.

Twichell, D.C. and Roberts, D.G., 1982, Morphology, distribution, and development of submarine canyons on the U.S. Atlantic Continental Slope between Hudson and Baltimore Canyons: Geology, v. 10, p. 408 412.