AmericanChemicalSociety.com

Granular media exhibit extraordinary properties due to their highly nonlinear and spatially discrete nature. In addition to their inherent theoretical interest, these materials are used or occur naturally in a wide array of settings. Our work is focused on pulse propagation in granular systems, a theme that arises in varied circumstances ranging from underground detection to shock absorption. In our previous report we presented results of an extremely successful binary collision approximation that allows analytic study of these systems and, most importantly, for the first time provides a theory with predictive capabilities. This latter outcome is important because pulse propagation behavior is affected by many parameters and it is thus difficult to gather a complete picture of the process if one is restricted to purely numerical results.

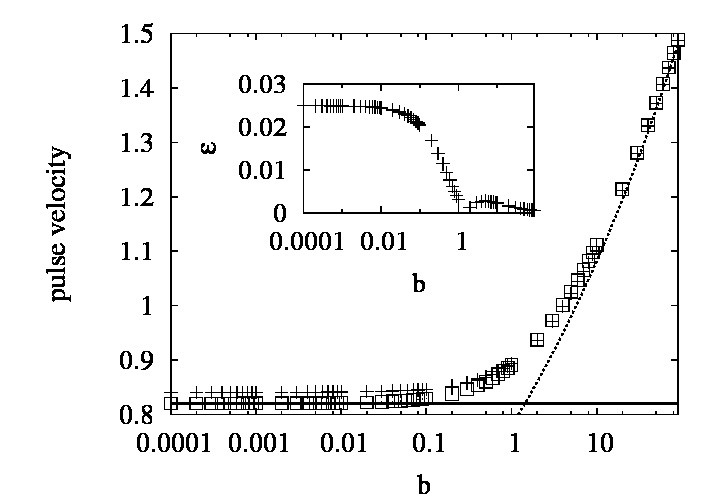
During this period we pursued three distinct areas of investigation. One of these was inspired by the availability of recent experimental results in a granular configuration different from those studied earlier: it consists of a chain of toroidal rings (o-rings) placed between rigid cylinders that act as nonlinear springs. For such granules, the purely repulsive force characteristic of dry granular materials is modified by the topological properties of the o-rings, leading to a potential that is now a combination of two contributions. One is the usual softer Hertz potential proportional to the compression to power 5/2 and the other is a hard potential proportional to the seventh power of the compression. Which of the two is dominant depends on the magnitude of the compression provided by the pulse as well as any precompression due to an external load such as gravity. We applied the binary collision approximation to this problem and found once again excellent agreement with simulation results, as illustrated in the adjacent figure. The figure shows the pulse velocity as a function of a parameter b that measures the relative contributions of the two portions of the potential. The theory fits the simulation results over the entire range, from the regime where the 5/2 contribution is greatly dominant to that in which the power 7 contribution dominates. The inset shows the error in the analytic theory, which is never more than 2.5%. This figure is for a situation without additional precompression. With precompression or gravity the agreement is not quite as good, but the error is never greater than 6-7% for any experimentally feasible case.

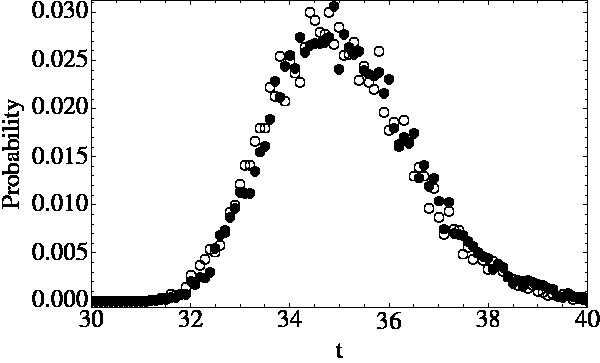
Our second focus was to introduce some randomness in the granular distribution in an effort to ultimately develop a theory that would allow the analysis of arbitrary granular distributions. Specifically, we studied pulse propagation in one-dimensional chains of spherical granules decorated with small randomly sized granules placed between bigger monodisperse ones. Such "designer chains" are of interest in efforts to control the behavior of the pulse so as to optimize its propagation or attenuation, depending on the desired application. We showed that our previously developed generalization of the binary collision approximation to simple decorated chains can be extended to chains decorated with small granules of randomly chosen radii. We showed that the new effective description can in fact provide analytic results for this system. In different realizations of the random chain problem, the time that it takes the pulse to reach a granule away from the origin is a random variable whose distribution is a reflection of the possible distribution of chain configurations. A typical illustration is shown in the adjacent figure, where we display the distribution of times to reach the 30th granule in a chain of 31 granules (thereby avoiding end effects). The filled circles are the predictions of our theory, and the empty circles are the results of numerical simulations. The agreement is clearly excellent, thus providing confidence in the analytic procedure.

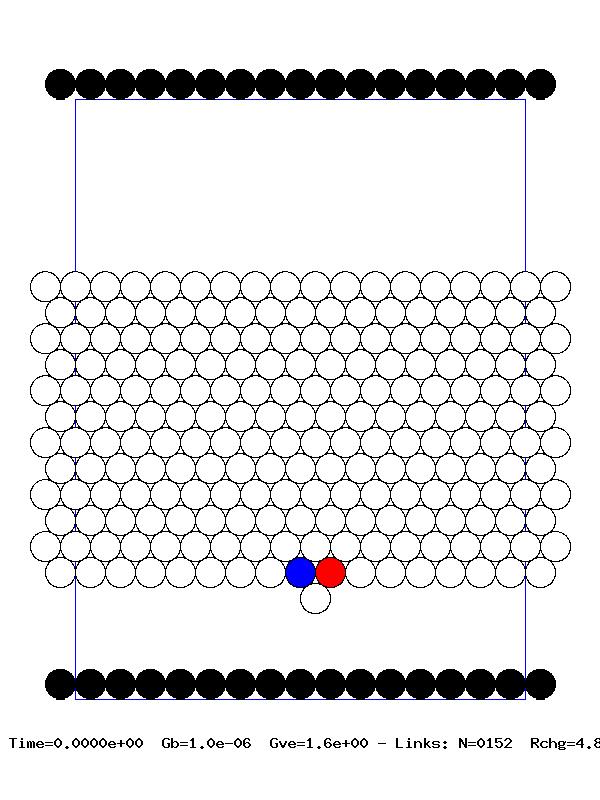
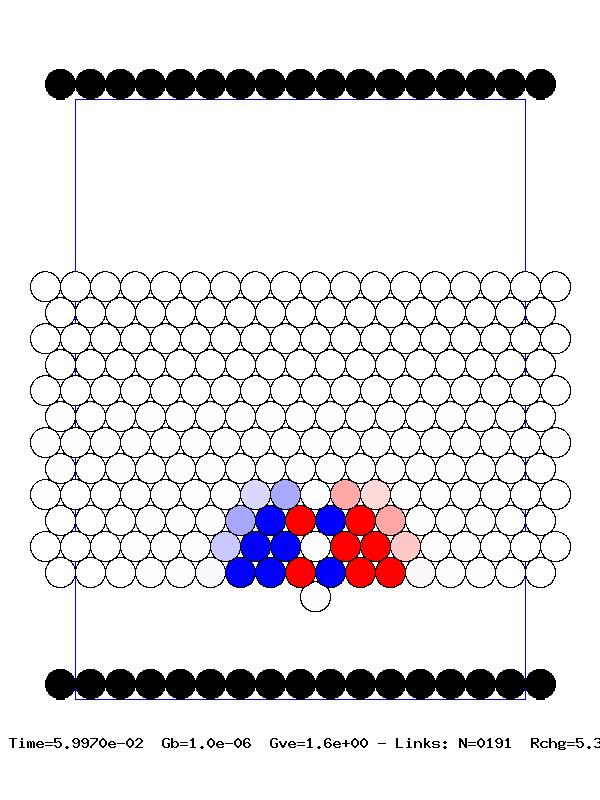
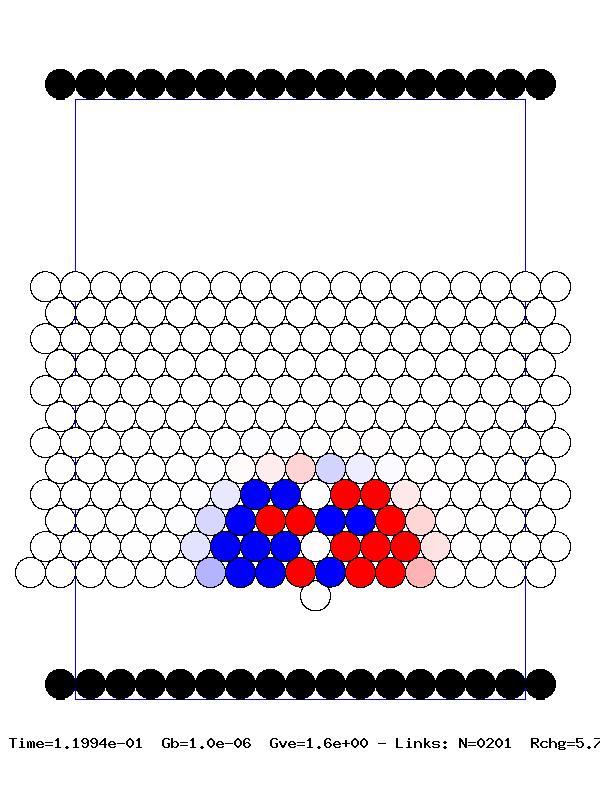
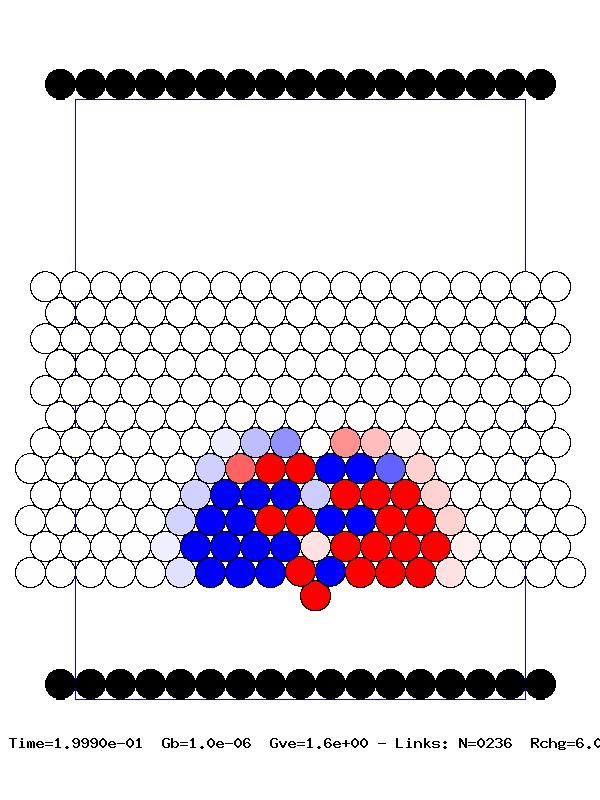
Pulse propagation in higher dimensional granular media is a considerably more difficult problem. We have begun to deal with these systems, necessarily numerically, by focusing on global properties. First we investigated the pulse propagation along a given observation direction. The decay in the velocity pulse was quantified by defining a restitution coefficient along this direction. This requires computing the relative velocities between two successive granules along the direction of pulse propagation. We observed that some of the pulse properties, such as pulse velocity and front velocity, exhibit global behavior, that is, they depend very weakly on the observation angle and pulse impulse angle. Next we investigated the time-dependent behavior of the the total kinetic and rotational energy in the system. The maximum pressure (force per granule in a given layer) on a given layer decays as the pulse propagates through the system. When the impact angle at which the initial energy is imparted to the system is non-zero, the pulse propagation is asymmetric, i.e., the mirror symmetry between the positive and negative horizontal axes is lost. This is directly related to the asymmetry in the force experienced by granules along this direction. We have quantified the asymmetry in the front propagation and are able to show that for large distances it tends to vanish. This indicates that for long times, due to the redistribution of the energy among increasingly large number of granules, the system loses memory of how the initial energy was delivered. One of the criteria for a better shock absorber is to maximize the energy conversion from the initial translational impact energy to the rotational energy in the system. Since rotation of a granule depends on the tangential force on it, we therefore need to maximize the surface friction. On the other hand, there is an upper limit on the possible tangential force (the well-known Coulomb condition). We thus reasoned that there must be an optimal value of the friction parameter that provides the best conversion of the initial translational energy to rotational energy. We have been able to compute this optimal value. A typical numerical experiment is illustrated in the adjacent frames. Blue indicates motion to the left, red to the right, and the intensity measures the magnitude of the velocity of each granule.