AmericanChemicalSociety.com

In the following, we will present the modeling work, and then discuss the measurements.

Modeling of Fickian diffusion coefficients of CO₂-water mixtures

The increase of CO₂concentration in the atmosphere is believed to affect global warming. Various options are being examined for storage of CO₂ from major sources. CO₂ storage in geological formations is perhaps the most attractive and practical option (Firoozabadi and Cheng, AIChE J., 2010). CO₂ injection in oil reservoirs for the purpose of improved recovery is also a partial short-term solution.

The effectiveness of CO₂ storage in saline geological formations, and CO₂-improved oil recovery depend on the rate of dissolution of CO₂ in the brine and in the oil (Hoteit and Firoozabadi, SPE J., 2009; Firoozabadi and Cheng, AIChE J., 2010). The rate of dissolution depends strongly on diffusion flux and consequently on diffusion coefficients. While there are limited data for CO₂-hydrocarbons over a wide temperature and pressure range, this is not the case for CO₂-water. Most of the data for diffusion of CO₂ in water are at temperatures less than 90°C. There are few data points for diffusion coefficients of H₂O-CO₂ system at pressures encountered at CO₂ sequestration in saline aquifers.

We have developed a simple model that accurately describes the infinite-dilution diffusion coefficients for CO₂ in water at both dilution limits. We also estimate the composition-based Fickian diffusion coefficients in CO₂-rich and water-rich mixtures. We account for the polar nature of water molecules and polarizability of CO₂ molecules. Water molecules have a large permanent dipole moment that causes formation of aggregates of its molecules. CO₂ has no net dipole moment, but due to its polarizability, it can have induced in the presence of an electric field. When a water molecule approaches a CO₂ molecule, a dipole-induced-dipole interaction is produced. The result is the formation of water-CO₂ clusters.

Our unified approach for infinite-dilution diffusion coefficients of CO₂-H₂O mixtures is based in part on the corresponding state principle. We take into account the temperature effect in the total dipole moment of water and the induced-dipole moment of CO₂, along with other thermodynamic variables. A single expression is found to describe diffusion coefficients of water infinitely diluted in CO₂ as well as CO₂ infinitely diluted in water as function of temperature, pressure, molecular mass, dipole moment, molar density and viscosity.

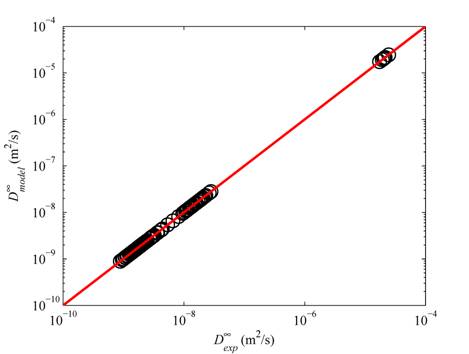
Figure 1 shows comparison of our model results with experiments based on 180 data points for 273 K ≤ T ≤ 368 K and 0.1 ≤ P ≤ 39.2 MPa and 8.9 × 10^-10 ≤ D^∞ ≤ 2.45 × 10^-5 cm²/s.

The model is then used to predict infinite dilution diffusion coefficients outside the range of data used for CO₂ -H₂O, and for propane-H₂O, pentane-H₂O, and H₂S-H₂O. The predictions are in agreement with data.

We have also used the irreversible thermodynamic approach (Ghorayeb and Firoozabadi, AIChE J., 2000) to predict the effect of concentration on diffusion coefficients of H₂O-CO₂ mixtures.

Figure 1. Diffusion coefficients of CO₂ and water at infinite dilution (D^∞)

Experimental Measurements of Thermal Diffusion and the Soret Effect Using a Deflected Laser Beam

Thermal diffusion arises when a temperature gradient is imposed across a material, and can cause either mixing or unmixing of the components.  Measurements are available in the literature for the thermal diffusion of liquid mixtures and large solute systems.  However, unanswered questions remain about the underlying physical phenomena, including the dependence on solvent interactions and the molecular size and shape of the components.  In practical applications, thermal diffusion can facilitate separations and provide sample characterization, as seen in thermal field flow fractionation for polymeric characterization (Weigand, J. Phys. Cond. Matt., 2004).

At the same time, measurements of the diffusion constant provide a basis for theoretical investigation of real mixtures.  Thermal diffusion can be an important aspect of reservoir modeling and simulations.

Our setup to measure thermal diffusion consists of a temperature controlled cell through which we pass a laser beam.  We impose a temperature gradient across the sample and monitor the resulting change in concentration by recording the deflection of the laser beam as a function of time.  Both thermal and molecular diffusion coefficients can be extracted from the deflection of the laser beam using established theory (Haugen and Firoozabadi, J. Phys Chem. B, 2006; Zhang, Briggs,Gammon, Sengers, J. Chem. Phys.,1996).

This past year we have rebuilt our experimental set-up and improved both the stability of the laser line and the closed loop temperature control system.  This set-up consists of two copper plates sandwiching a quartz glass ring.  The temperature on the copper plates is controlled through an electric circuit consisting of power supplies directing current through thermofoil heaters on each plate.  The setup is controlled in a close loop fashion through PID software run through LabView, which allows for all aspects of the experiment to be monitored and controlled simultaneously.  The implementation of this closed-loop computer control system has resulted in tight temperature control on the copper plates.  Figure 2 shows the PID-controlled temperature on the top and bottom plates.  Figure 3 shows the imposed temperature difference, stable to within 2.3 mK, which can be turned on and off many times in a row, to allow for a more thorough assessment of the experimental measurements. 

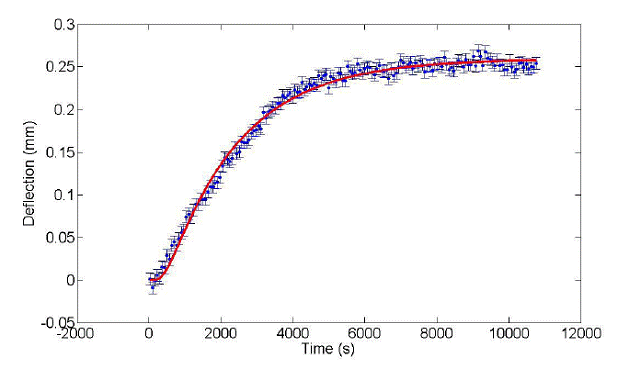
Testing demonstrates that the setup is working properly.  Measurements of an equimolar mixture of hexane and toluene give a Soret coefficient of S_T = 4.6x10^-3 K^-1, which paramaterizes the fit shown in Figure 4. This value is within 5% of other laser-beam deflection measurements on the same system.  During the coming months we intend to extend measurements using this setup to novel systems.

\s

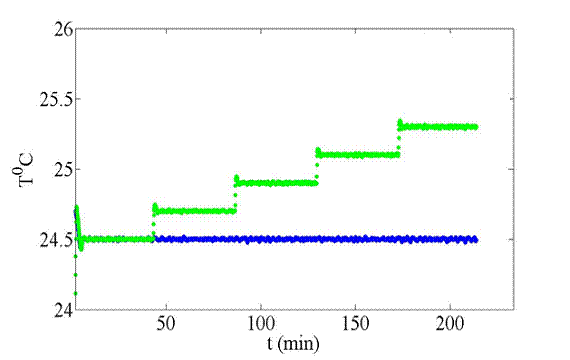
Figure 2: The temperature on the top plate is shown in green, and the bottom plate in blue, controlled by thermofoil heaters and a PID loop, for approximately 3.5 hours.

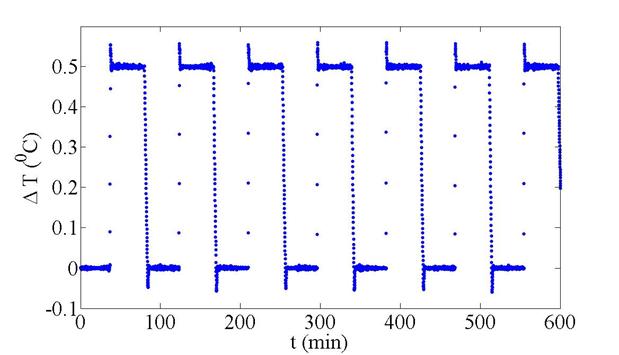
Figure 3:  The temperature gradient between the two plates can be stably turned on and off for many cycles at a time.

Figure 4: Laser beam deflection in an equimolar mixture of hexane and toluene, given an imposed temperature gradient of 0.5 °C.