Pattern Formation in Spatially Structured Active Media: Theory and Simulations

Reports: ND6 49010-ND6: Pattern Formation in Spatially Structured Active Media: Theory and Simulations

Bulbul Chakraborty, PhD, Brandeis University

This New Direction grant launched my research on spatially structured, excitable chemical media. We have achieved a number of new results on the behavior of repulsively coupled chemical oscillators, and made significant progress in developing a framework for stochastic differential equations that model reaction-diffusion systems. The coupled oscillator work is being submitted to Physical Review E [cond-mat/arXiv:1009.6004].

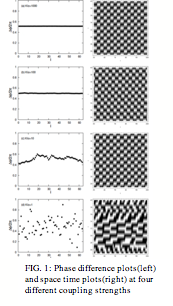
FIG. 1: Phase difference plots(left) and space time plots(right) at four

different coupling strengths

Coupled Chemical Oscillators: This theoretical/simulation study was directly motivated by experiments performed by Irv Epstein (Co-PI) and Seth Fraden. The experiments studied arrays of microdrops containing the reactants for the BZ (Belousov-Zhabotinsky) reaction. The coupling between the droplets, through the diffusion of the inhibitor, led to a multitude of interesting patterns [[J. Phys. Chem. Lett. 1, 1241-1246 (2010)]]. We started with a minimal model to see how much of the pattern formation could be understood from the geometrical frustration that arises in oscillators that would like to be p out of phase but are placed on a lattice on which that pattern cannot be achieved globally, for example, on a hexagonal array. We numerically solved the differential equations arising from phase oscillators with random (Gaussian-distributed) frequencies, coupled repulsively through nearest neighbor interactions on a 1D chain, 1D ring, and on a 2D hexagonal array.

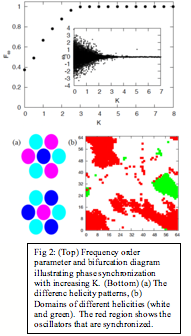
Brief Summary of Results: In 1D, we have shown using linear stability analysis as well as numerical results, that the stable phase patterns depend on the geometry of the lattice. We also show that a transition to the ordered state does not exist in the thermodynamic limit. In two dimensions, we have shown that the geometry of the lattice constraints the phase difference between two neighbouring oscillators to 2p/3, and that domains of opposite helicities (Fig. 2) get frozen in as the frequencies synchronize. Michael Giver and Zahera Jabeen have been the researchers primarily responsible for this project. Mitch Mailman helped design the project in its initial stages, and Dapeng Bi is working on the model with amplitude variations. We have studied the coupled oscillator system using tools that are more commonly used in condensed matter physics in the context of phase transitions. These tools have proven to be really beneficial in understanding the emergence of phase and frequency coherence in these coupled oscillators. We will continue to push these techniques in analyzing more complicated models of coupled oscillator systems.

Patterns on 1D ring: When the coupling between the oscillators is turned off, each of the oscillators in the system will evolve in time according to its own frequency, w_i. As we switch on and increase the coupling, we observe the oscillators to form local frequency entrained clusters. As the coupling is increased further, the clusters merge with one another until eventually, at some critical value of the coupling constant, all of the oscillators are entrained with a common frequency. Fig. 1 gives a qualitative picture of the synchronization (or desynchronization) process in a system of 64 oscillators. The figure shows four space-time plots over a range of effective coupling constants (K/s) and a corresponding plot of the phase difference as a function of position on the lattice. At low coupling both the frequencies and phases are disordered. As the coupling is increased to K/s = 10, we can see that all the oscillators evolve with approximately the same frequency, but maintain some disorder in the phase relationships. It is not until a coupling strength two orders of magnitude larger that we see perfect phase ordering at this system size. The experimental microdrop setup shows a pattern very similar to the fully synchronized (antiphase) pattern. We have studied frequency and phase synchronization, quantitatively by measuring appropriate order parameters.

Fig 2: (Top) Frequency order parameter and bifurcation diagram illustrating phase synchronization with increasing K. (Bottom) (a) The differenc helicity patterns, (b) Domains of different helicities (white and green). The red region shows the oscillators that are synchronized.

Patterns on a Triangular Lattice: On a triangular lattice, the optimal local pattern of nearest-neighbor oscillators locking into a p phase difference is incompatible with the geometry. Results from our numerical simulations show that the frequencies synchronize beyond a critical coupling strength (for a finite size system), however the phase pattern remains disordered with domains of different helicities frozen in. The steady state is, therefore, one where the whole array oscillates with the same frequency but with no long-range order in the phase pattern. This is a glassy state with features that are similar to disordered statistical systems such as spin glasses. We [Dapeng Bi, Zahera Jabeen, and Bulbul Chakraborty] are in the process of studying extensions of our model that allow amplitude fluctuations in order to see if that relieves the frustration and leads to an ordered phase pattern.

Lattice Models of Reaction-Diffusion Systems Theoretical studies of chemical oscillations broadly fall into two categories: (1) a rate equation approach in which the reactants are assumed to be well mixed, and (2) a partial differential equation approach in which spatial dependence is taken into account by adding diffusion terms to the rate equations. These two approaches explain qualitatively the experimental phenomena. But it is well known that for reaction diffusion systems, often just adding a diffusive term to the rate equations does not give the correct quantitative answers, especially in low enough dimensions [U. C. Tuber, M. Howard, and B. P. Vollmayr-Lee, J. Phys. A 38, R79 (2005]. There are usually additional multiplicative noise terms arising due to intrinsic number fluctuations in the system. This will be especially relevant for the micro droplet experiments where there is finite probability for low concentration of reactants. Michael Giver visited India and worked with Rajesh Ravindran to implement a Gillespie algorithm for simulating reaction diffusion systems on a lattice, and to begin the process of applying field theoretical techniques to construct coarse-grained equations and correlation functions from these lattice models.