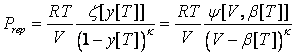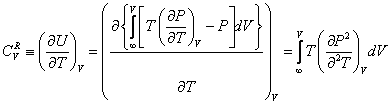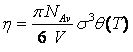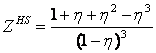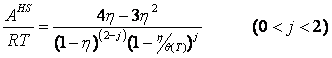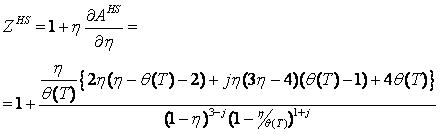AmericanChemicalSociety.com

The narrative progress report

    One of the most important projects of the research strategy listed in the original proposal is evaluation of the temperature dependencies for the developed Equation of State (EoS). This equation originates from the hard-sphere approach, which claims the temperature-independent covolume b. However, real molecules do not have hard repulsion potentials. This fact has been considered by several theoretically-based models, including different modifications of SAFT, which have introduced temperature dependencies for their size parameters. In fact, such dependencies may substantially increase the flexibility of EoS and, theoretically, allow a simultaneous fitting of the volumetric properties of real compounds, their vapor pressures, and the virial coefficients. An important issue that should be considered prior further development is the consequences of making the covolume temperature-dependent for the isochoric heat capacities.

   Most of theoretically-based models for hard spheres and hard discs can be generalized as follows:

                                                          (1)

where k is an arbitrary positive number, b[T] is a temperature-dependent co-volume, z and y are arbitrary functions. Remarkably, the expression for y[T] could be different that eq 2. Thus, the models yielding the correct value of the packed density might be also generalized by eq 1. The isochoric heat capacity is given as:

                                  (2)

Let us analyze the function . If this function has a positive infinity value, then after substitution into eq 2 the non-physical negative infinite value of  will be obtained, and visa versa. Substitution of eq 1 into the function above yields:

                             (3)

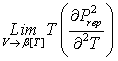
It can be seen that the sign of eq 3 depends only on the sign of y, because b[T] must always be positive. However the negative y at the density limit is also non-physical because it yields the negative infinite value of pressure (see eq 1). Thus, at the infinity pressure  obtained from eq 1 always has a negative infinity value. In other words, the concept of the effective hard sphere diameters and the temperature-dependent co-volumes is responsible for prediction of non-physical phenomena, regardless of the kind of temperature dependence and the expression for y used.

     Thus, it can be seen that the temperature-dependent covolumes are the major factor responsible for the numerical troubles. Let us consider the temperature dependent reduced density of a single segment is given as:

                                                                                                   (4)

q(T) is the temperature dependence. The Carnahan-Starling's expressions for the hard sphere repulsive contributions are:

                                                                                             (5)

                                                                           (6)

It can be seen that these contributions approach infinity at h ® 1 and the model's covolume is therefore hV. Since q(T) decreases with temperature, the covolume of Eqs. (4-5) decreases with temperature as well. Let us rewrite Eq. (6) as follows:

                                                 (7)

Eq. (7) approaches infinite two times: at h ® 1 and at , while . Hence,  represents the covolume of Eq. (7) and it is temperature-independent. The smaller volumes (including hV) obviously have no physical relevance anymore. The compressibility factor is yet given as:

                      (8)

Taking j = 0 Eq. (5) is recovered.

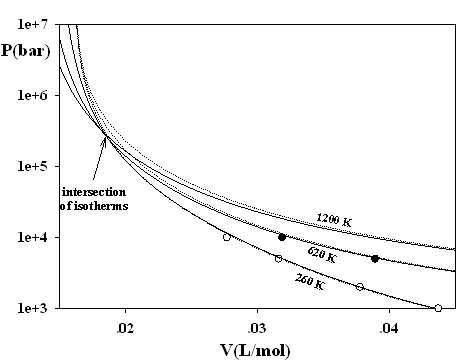
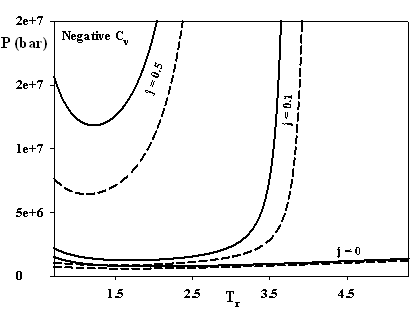
     Figure 1 demonstrates that already a small value of j = 1/3 solves the problem of isotherms intersections. In addition, j has a remarkable effect on the non-physical predicting on the negative isochoric heat capacities, which are restricted now to astronomic pressures and low temperatures irrelevant for fluid phases (see Fig. 2).

Figure 1. Three isotherms of methane: solid lines – original SAFT of Chapman et al. (Ind. Eng. Chem. Res. 29 (1990), 1709-1721) with j = 0. Dotted lines SAFT of Chapman et al., attached by eqs. (7-9) (j = 1/3, s = 3.71001 Å, e/k = 154.188 K).

Figure 2. Lines of zero C_V as function of j: dashed lines – the SAFT of Chapman et al. (Ind. Eng. Chem. Res. 29 (1990), 1709-1721), solid lines – SAFT-VR-SW of Gil-Villegas et al. (Chem. Phys. 106 (1997) 4168-4187).

         Although this undesired phenomenon is not completely vanished yet, further progress could be achieved with the appropriate formulation of the model (see for example the difference between the SAFT of Chapman et al. and SAFT-VR-SW).

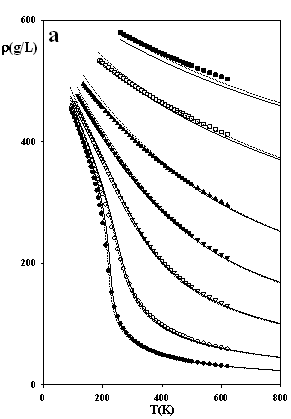
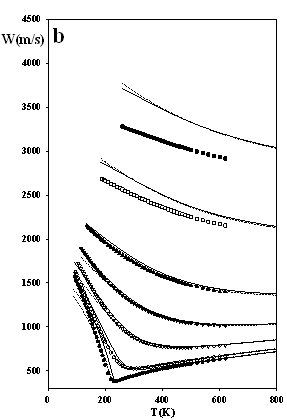
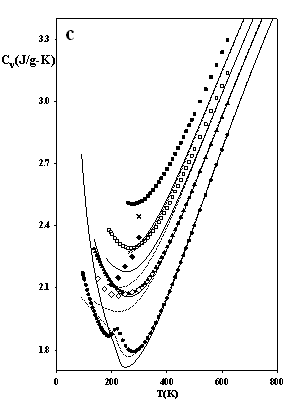
     Figure 3 depicts predictions of the densities, heat capacities and the sound velocities at j = 1/3, and they appear to be particularly accurate. These results indicate that the issue of numerical pitfalls can be treated with no noteworthy affection of the model's accuracy.

Figure 3. The thermodynamic properties of methane at high pressures as predicted by SAFT EOS models attached by eqs. (7-8): dotted lines – SAFT-VR-SW (j = 1/3, s = 3.69611 Å, e/k = 162.218 K, l = 1.475) solid lines – SAFT of Chapman et al. (j = 1/3, s = 3.71001 Å, e/k = 154.188 K) Experimental data: ● – 100 bar, ○ – 200 bar, s – 500 bar, q – 1000 bar, p – 2000 bar, □ – 5000 bar, ■ – 10,000 bar;  ¯ – 2000 bar; z – 5000 bar; Ï – 10,000 bar