AmericanChemicalSociety.com
Reports: DNI8 49083-DNI8: Investigation of Crack-Wake Effects on Fracture Toughness of Geological Materials
Spandan Maiti, Michigan Technological University
ABSTRACT
An improvement in the fundamental understanding of crack propagation in geological formations will contribute to advancement of knowledge and help in hazard mitigation and extraction of natural resources. Current approaches to modeling crack propagation consider mostly phenomena occurring ahead of the crack tip. However, the significant effect of microstructures present at the crack wake remains unaddressed, resulting in incomplete understanding. We pursued a research program to advance the fundamental understanding of crack propagation in geological materials by following a central hypothesis that the effective fracture toughness of geological material is significantly altered by the presence of microstructural features at the crack level, operative at the wake of the propagating crack. Novel numerical algorithms have been developed to simulate arbitrary fast crack propagation in a domain, as well as the sensitivity analysis of various input parameters on the output.
INTRODUCTION
Our central hypothesis for the proposed research is that the microstructural features at the crack level are operative at the wake of the propagating crack and it significantly alters the effective fracture toughness of the material. Unlike in homogeneous materials, a crack cannot propagate in its own plane in face of these heterogeneities thus giving rise to the crack surface features mentioned above. We proposed to test the central hypothesis by evaluating the effect of both grain bridging and presence of pre-existing flaws on crack propagation, and quantify their effect on the fracture toughness. This endeavor resulted in two computational challenges: (1) A computational technique for arbitrary fast crack propagation in a domain, and (2) development of sensitivity analysis technique to study the effect of microstructural features on fracture toughness. To address the first challenge, we developed a new technique called Generalized ‚ohesive Element (GCE) method within the framework of finite element analysis that can nucleate and propagate a fast crack in an arbitrary direction. For the second challenge, we have developed an ANOVA decomposition based algorithm that can compute the sensitivity indices for input parameters for a given output. These two directions will be discussed briefly in subsequent sections.
RESEARCH ACHIEVEMENTS
In the presence of heterogeneities, a crack in a geological material can deflect out of its plane that can significantly affect the apparent fracture toughness. We have developed a novel computational technique to simulate arbitrary crack motion in a domain. Salient features are discussed below:
Generalized Cohesive Element (GCE) modeling: An alternative approach to the classical theory of fracture mechanics is the cohesive zone modeling. However, typical cohesive element algorithms are restricted to the edges of the finite elements, thus making the potential crack path mesh dependent. We have developed a new technique that can pass a crack through a finite element, thus approximating actual crack path closely. The original element is split (Figure 1) into two child elements to allow for the crack path within the element. Cracks are nucleated whenever maximum principal value reaches the failure strength of the material. Once nucleated, it can propagate through adjacent elements subjected to the satisfaction of the failure criterion. The direction of
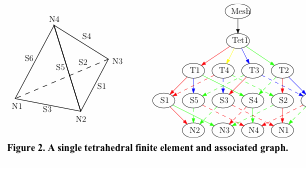
| Figure 2. A single tetrahedral finite element and associated graph. |
 maximum principal stress
determines the direction of crack propagation.
maximum principal stress
determines the direction of crack propagation.
Mesh topology: Most challenging feature of the said technique is the enumeration of mesh topology. As new child elements are created, the topology of the finite element mesh changes continually, and element connectivity table need to be updated continuously. We have devised an efficient way to handle the resulting dynamic data structure. The mesh is represented as a graph as shown in Figure 2, and all the cutting and duplication operations, that give rise to the changing topology, are performed on the graph itself. The connectivity table required for finite element computations can be extracted from the graph at any point.
Sensitivity analysis: The computational model is represented as ANOVA decomposition with the coefficients of the expansion as the variances of different input parameters:
![]()
In the above
equation, the term f0 gives
the mean effect which is a zeroth-order constant. The first order term fi (xi) gives the
individual contribution of an input variable xi on the output where as the second order term fij(xi,xj)
gives the cooperative effects of the input variables xi and xj.
Typically for physical systems, terms higher than second order are weak, and
can be neglected. The first order terms are the variances of the input parameters,
while second order terms are the joint variances. Thus, the sensitivity of the
input parameters on the output can be found from this expression. The terms are
evaluated by a set of model runs.
PROJECT OUTCOME Figure 3. Simulations of arbitrary crack path with generalized cohesive elements.
 The grant has supported one
Masters student partially, and has resulted in one journal publication, one
conference presentation. One Masters thesis and one more publication are being
finalized. This endeavor has established dynamic fracture of quasi-brittle
materials as a primary thrust area of PI's research. As a synergistic effect,
the developed algorithms have been used for another Masters thesis and a
journal publication manuscript. The grant has prepared the PI to establish
himself as a primary researcher in the field of dynamic response of materials,
and has resulted in two more grants from different organizations. The grant has
helped the PI to pursue his long-term goal of becoming an eminent researcher in
the field of dynamic fracture of quasi-brittle geological materials. We are
currently using the developed algorithms to simulate the effect of microcracks
and grain bridging on the apparent fracture toughness of a dominant crack. This
endeavor will help understand the effect of heterogeneities in the medium on
the propagation of a fast crack, which is a typical scenario in geological materials.
The grant has supported one
Masters student partially, and has resulted in one journal publication, one
conference presentation. One Masters thesis and one more publication are being
finalized. This endeavor has established dynamic fracture of quasi-brittle
materials as a primary thrust area of PI's research. As a synergistic effect,
the developed algorithms have been used for another Masters thesis and a
journal publication manuscript. The grant has prepared the PI to establish
himself as a primary researcher in the field of dynamic response of materials,
and has resulted in two more grants from different organizations. The grant has
helped the PI to pursue his long-term goal of becoming an eminent researcher in
the field of dynamic fracture of quasi-brittle geological materials. We are
currently using the developed algorithms to simulate the effect of microcracks
and grain bridging on the apparent fracture toughness of a dominant crack. This
endeavor will help understand the effect of heterogeneities in the medium on
the propagation of a fast crack, which is a typical scenario in geological materials.
Copyright © American Chemical Society

