AmericanChemicalSociety.com

In principle, quantum chemistry is not difficult; after all, it requires solving only a single well-defined equation, the Schršdinger equation.  Yet, for chemical systems where more than a handful of electrons are involved, even high-power computers cannot manage to solve this equation exactly.  This is why the majority of quantum mechanical simulations of chemical dynamics rely on pseudopotentials, which greatly reduce the number of electrons that need to be explicitly considered in a quantum mechanical calculation.  The pseudopotential method is based on the idea that in any chemical system, only a few electrons (e.g., valence electrons) are of interest to the problem at hand, so that the effect of the remaining electrons (e.g., core electrons) can be treated implicitly via an effective potential.  The use of effective potentials is a necessity for chemical dynamics simulations, in which the Schršdinger equation for the electrons must be solved over and over again as the nuclei move and the chemical bonds rearrange.  The hard part is coming up with an effective potential that allows the physics of the implicitly-treated electrons to be described well enough to ensure that the chemical dynamics associated with the explicitly-treated electrons are accurate. 

In most chemical dynamics simulations, the effective potentials employed are developed empirically:  in other words, the effective potentials are simply made up and then adjusted to try to reproduce properties of the system of interest that are known from experiment.  Recently, we developed a method that allows the effective potential to be calculated from the known quantum mechanics of the system (C. J. Smallwood, R. E. Larsen, W. J. Glover and B. J. Schwartz, "A Computationally Efficient Exact Pseudopotential Method. I. Analytic reformulation of the Phillips-Kleinman Theory," J. Chem. Phys. 125, 074102, 1-8 (2006)).  Our method is based on the Phillips-Kleinman (PK) theory, which provides a framework for deriving an effective potential with the guarantee that the wavefunction of the explicitly-calculated electrons is orthogonal to those of the implicitly-treated electrons; this orthogonality, which is part of Pauli's Exclusion Principle, is a key requirement of quantum mechanics.

The chief failing of the PK formalism, including our extension of it, is that the effective potential is calculated only for a single configuration of the system under study, a limitation known as the Frozen Core Approximation (FCA).  For example, the PK formalism provides only a single effective potential for the bonding electrons of a diatomic molecule, independent of whether the molecule is at equilibrium or the two atoms are nearly dissociated.  It is well known that the energies of the bonding electrons in molecules are not adequately described by simply adding together the effective potentials of the valence electrons on the constituent atoms; this problem arises from the fact that the effect of the core electrons on the valence electrons changes as chemical bonds are formed or broken.  The focus of our theoretical work over the past few months has been to develop a new method that goes beyond the FCA:  we have been working to develop rigorous PK effective potentials that can respond to changes in the physics of the system.  In this way, the effective potential felt by the bonding electrons in a diatomic molecule changes as a function of the distance between the two atoms in the molecule, providing a rigorous description of chemical bonding all the way from equilibrium to the dissociation limit.  We believe that once complete, our formalism will help to revolutionize pseudopotential theory, making accessible a wide variety of quantum dynamics simulations of complex systems that are currently beyond the realm of computational feasibility. 

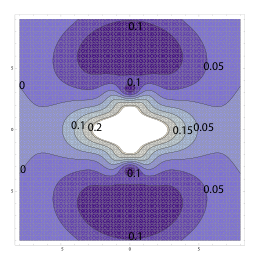
To accompany our experiments on KH and other simple alkali-based diatomics in solution (described in previous reports), we have started by correcting known atomic effective potentials to accurately describe the chemical bonds of alkali-based diatomic molecules.  At the dissociation limit, the effective potential of the valence electrons in the diatomic is well described by the sum the effective potentials of the atoms.  What we have done is use our extended PK method to calculate the effective potential of a diatomic molecule as a function of the distance between the nuclei.  In this way, we have determined how the effective potential varies smoothly between that of the isolated atoms and that of the equilibrium bonded molecule. Figure 1 shows an example of the "correction function" that we have determined for the potential needed to accurately describe the bonding properties of the Na₂ molecule at its equilibrium distance; this function is what must be added to the individual sodium atomic effective potentials to get a rigorously correct quantum description of the Na₂ molecule.  We are currently working to describe this correction term analytically as a function of the distance between the two atoms.  Although the determination of this distant-dependent term in the effective potential is computationally expensive, since it must be repeated at every possible bond distance, this set of calculations needed to be done only once.  This is because once we have an analytic expression for the new term in hand, it can be employed directly in quantum dynamics simulations, providing an enormous computational advantage compared to solving the full Schršdinger equation at every MD time step. 

Figure 1:  Contour plot of the "correction function" that must be added to the individual atomic effective potentials to correctly describe the bonding properties of the Na₂ molecule at its equilibrium bond distance.  The axes are in bohr (1 bohr = 0.53 ) and the energy contours are in hartree (1 hartree = 27.2 eV).  The origin is at the molecular center-of-mass, and the two Na nuclei are located in the centers of the small circular regions labeled by the 0.1 hartree contour.