AmericanChemicalSociety.com
Reports: DNI9 48950-DNI9: Three-Dimensional Fragmentation of Core-Annular Flow
Haoxiang Luo, PhD, Vanderbilt University
1. The objectives and completed tasks
In the proposal, the following specific objectives have been proposed for a two-year period:
- Develop a code for modeling the three-dimensional core-annular flow,
where the fluid-fluid interface will be handled by the immersed-interface
method and the topology change due to the fragmentation of the core phase
will be incorporated.
- Incorporate the interfacial transport of a surfanctant into the code.
- Characterize the topology of the interface for a range of parameters
governing the core-annular flow.
During the first year of this project, objective 1 was being pursued. The original goal of modeling the two-phase flow in a cylindrical pipe is extended to modeling the flow in arbitrary geometries. This is motivated by the fact that the real-world pipeline system often consists of non-cylindrical devices such as fittings and valves and these complex geometries have a significant effect on the stability and breakup of the core-annular flow.
To handle the arbitrary shape of the pipe wall, a recently developed sharp-interface immersed-boundary method was used. Like the immersed-interface method for the fluid-fluid interface, the sharp-interface method is also based on the Cartesian grid. Therefore, a single-block Cartesian grid is employed to treat both the fluid-fluid and the fluid-solid interfaces, though the two approaches of treatment are quite different.
To handle the interface breakup and the topological change, two approaches are currently being explored. In the first approach, a set of marker points that convect with the fluid are used and the interface is discretized by a set of linear triangular elements. An adaptive algorithm is being incorporated to adjust the surface resolution and to change the connectivity of the mesh with prescribed merging/breakup criteria. In the second approach, a level-set function is being Incorporated to track the interface. The accuracy of the two approaches will be compared.
2. Details of the numerical method
2.1 Treatment of the fluid-fluid interface
The two-fluid interface and the discontinuity across the interface are
handled by the immersed-interface method (IIM) initially developed by
Peskin, as described in the proposal. A 3D method has
implemented to solve the generalized Navier-Stokes equation in the
Cartesian coordinates,
(1)
where Dirac's delta function is approximated in the simulation by a narrowly spread but smooth function.2.2 Treatment of the fluid-solid interface
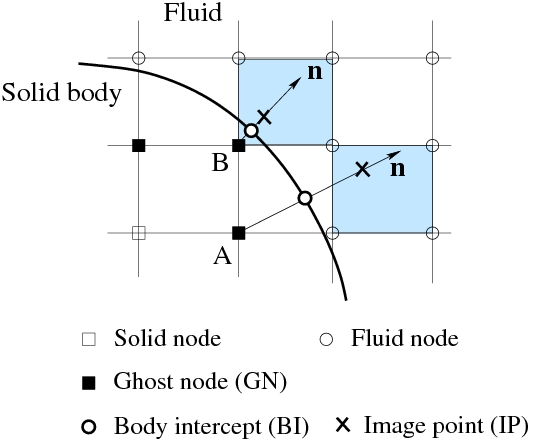
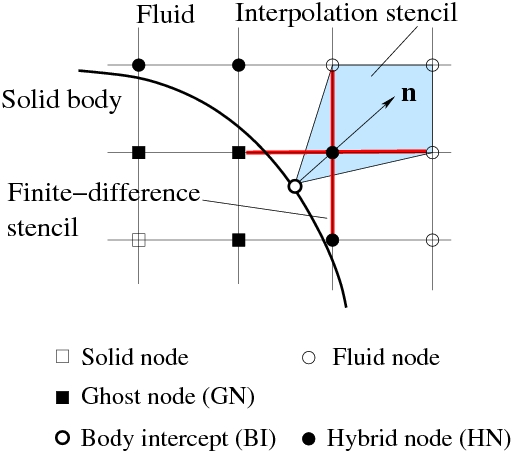
To treat the no-slip and no-penetration boundary conditions at the solid surface, a sharp-interface immersed-boundary method developed by our group at Vanderbilt University is applied. The method is based on a former immersed-boundary implementation. In this method, the fluid-solid interface is represented by an unstructured surface mesh composed of triangular elements. The marker points on the mesh are Lagrangian points which follow the motion of the fluid at the interface (in the case of moving boundaries). Since the finite-difference stencil can not be used as usual for the nodal points near the solid boundary, definitions of ``ghost nodes'' and ``hybrid nodes'' are introduced to facilitate both the flow field interpolation and the finite-difference discretization (Fig. 1).
2.3 Two approaches for interfacial breakup
Two approaches are being explored for handling the interfacial breakup. In the first approach, the Lagrangian makers and an unstructured surface mesh are used to track the interface. A previous adaptive, local surface-fitting algorithm is adopted to refine the mesh at the location of the neck where the fluid filament tends to break up. The second approach incorporates the level-set function for surface tracking. The level-set function is updated according to a convection equation. Currently, the level-set method is being implemented in our immerse-boundary code to handle the merge and breakup of the interface.
2.4 Exploration of the parallel algorithm
The three-dimensional flow simulation will be in general cost-prohibitive. To accelerate the program, parallel algorithms were explored. A sparse linear system solver, AZTEC, developed by the Sandia National Laboratory was tested. Currently, the parallel solver can run on 64 to 128 processors with good performance. Further improvement of the code scalability is being pursued.
3. Result demonstration
To validate our solver with two types of immersed-boundary methods
incorporated, we ran a series of simulations of a 3D droplet
deformation in simple shear flow and compared the results with the
experimental data. The problem is governed by two nondimensional
parameters: the droplet to ambient fluid viscosity ratio ![]() ,
and the capillary number
,
and the capillary number
![]() , where
, where
![]() is the shear rate and
is the shear rate and ![]() the surface tension.
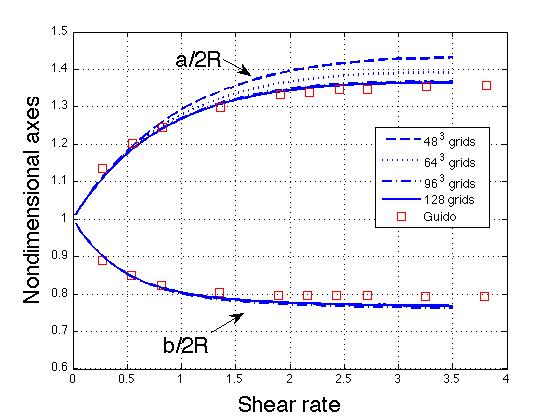
The comparison in Fig. 2 shows that as the grid is
refined, the numerical simulation agrees very well with the
experiment.
the surface tension.
The comparison in Fig. 2 shows that as the grid is
refined, the numerical simulation agrees very well with the
experiment.
|
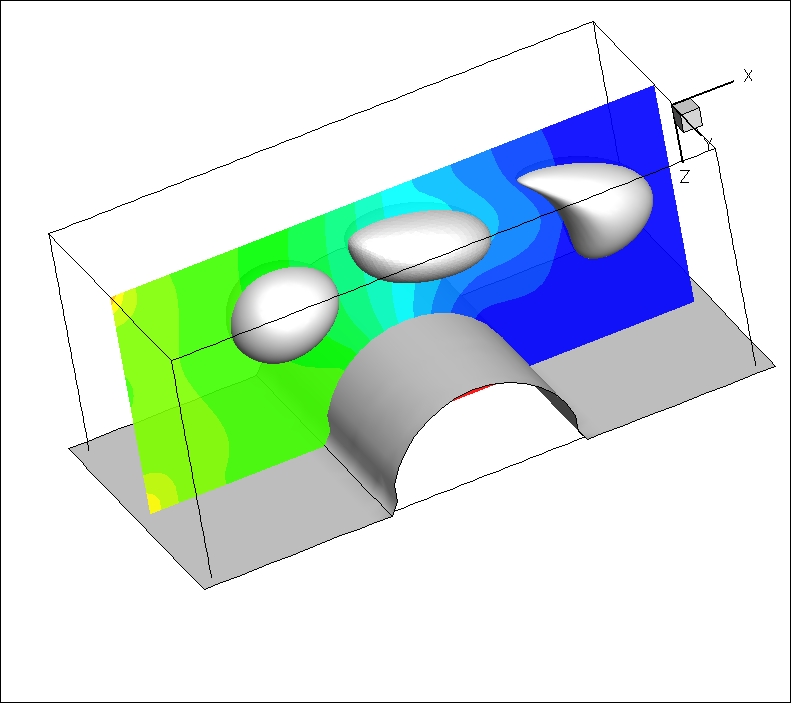
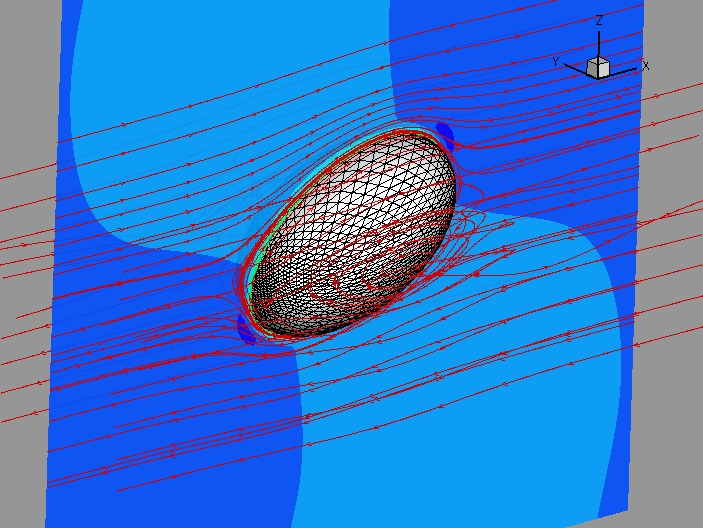
A demonstration case is shown in Fig. 3, where a 3D droplet goes through the narrow portion of a channel while being deformed. A single-block Cartesian grid is used here to discretize the entire domain including the channel and the droplet.
3. Educational aspect
A graduate student, Mr. Bo Yin, was support by this grant in the past year, who received extensive training in theoretical and computational fluid dynamics. The physics of multiphase flow and computational modeling are currently being incorporated into undergraduate/graduate course, Intermediate Fluid Mechanics, that the PI teaches at Vanderbilt University. In this course, the students learn to use software COMSOL Multiphysics to model several common flow problems including the single- and two-phase flows, low- and high-Reynolds number flows, and heat transfer.
Copyright © American Chemical Society


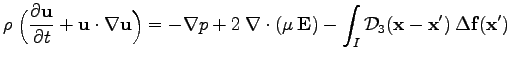 d
d