Back to Table of Contents

46584-G10
Inorganic Guest Species in Organic Crystals: A First-Principles Investigation

Anton Van der Ven, University of Michigan

Overview and motivation

New organic electrode materials have the potential to dramatically expand the applicability of battery technology to new sectors such as automotive transport. Organic electrodes in rechargeable batteries must be able to intercalate ionic species that are either shuttled between electrodes or extracted from the electrolyte. The ability to design organic molecular building blocks with precisely defined electronic and steric features enables the synthesis of organic solids having electrochemical, kinetic and mechanical properties specially tuned for a specific battery application. However, before the rational design of such materials is possible, a fundamental understanding about the electronic, thermodynamic and kinetic properties of guest elements within various electronically conducting organic solids is essential. First-principles electronic structure methods can play a pivotal role in elucidating the mechanisms of charge transfer between electron donating or withdrawing guest species in electroactive organic crystals as well as rationalizing thermodynamic stability of and ionic mobility within organic electrode materials.

Accomplishments of the first year

During the first year of this Petroleum Research Grant, we have devoted our efforts to developing an automated statistical mechanical software tool to predict phase diagrams and diffusion coefficients in intercalation compounds with arbitrary crystallographic complexity. This tool is essential to enable a systematic study of the thermodynamic and kinetic properties of different electronically conducting organic compounds.

As a first test case, we applied the software tool to predict the temperature composition phase diagram and lithium diffusion coefficient in Li_xTiS₂. Our approach uses atomic-scale energies from first principles to parameterize an easily evaluated cluster expansion Hamiltonian, which can then be used in thermodynamic (Monte Carlo) and kinetic (kinetic Monte Carlo) simulations to determine diffusion constants. A Kubo-Green formalism is used to calculate diffusion coefficients for interstitial diffusion in the non-dilute regime with kinetic Monte Carlo simulations. We applied this formalism to predict the finite-temperature thermodynamic properties of Li_xTiS₂ as well as its concentration dependent Li diffusion coefficients.

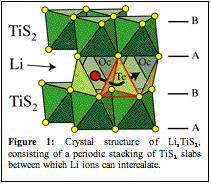
The sulfur atoms of LiTiS₂ form two-dimensional triangular lattices stacked in an ABAB sequence, leading to a hexagonally close-packed anion sublattice. The Ti and Li ions alternately fill octahedral sites between the close-packed sulfur planes. The crystal can be viewed as an array of TiS₂ slabs separated by layers of Li (see Fig. 1)

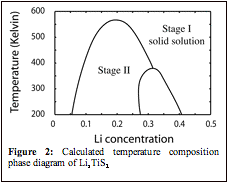
The electrochemical removal of Li from LiTiS₂ results in the creation of Li-vacancies between the TiS₂ slabs, introducing configurational disorder. Monte Carlo simulations applied to the cluster expansion allows us to construct a phase diagram depicting phase stability as a function of Li concentration and temperature. Figure 2 illustrates the calculated phase diagram for Li_xTiS₂ between 200 K and 600 K..

Li diffusion in intercalation compounds occurs by a vacancy mechanism, whereby individual Li ions hop into neighboring vacant sites. Crystallographically, the least constricted pathway for Li migration between neighboring octahedral sites of layered transition metal sulfides having the O1 crystal structure is through an adjacent tetrahedral site. This is schematically illustrated in Fig. 1.

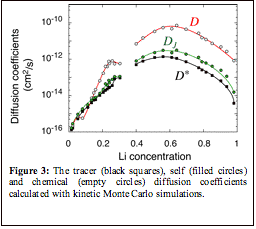To calculate diffusion coefficients at finite temperature, we used a standard kinetic Monte Carlo algorithm. Figure 3 illustrates calculated diffusion coefficients at 300 K as a function of Li concentration. As is clear from Fig. 3, the diffusion coefficients all have a very strong dependence on Li concentration, exhibiting a maximum close to x=0.5 and varying by several orders of magnitude over the whole concentration interval. The diffusion coefficients, decreases rapidly as the Li concentration is reduced below x=0.55. The kinetic Monte Carlo simulations show that Li transport is dominated by hops into divacancies. The migration barriers associated with divacancies are significantly lower than those into isolated vacancies (which involve tetrahedral sites that share a face with an occupied octahedral site). However, the divacancy concentration is very low at high Li concentration, increasing with decreasing Li concentration. Below x=0.55, the diffusion coefficients decrease in spite of the continued increase in the number of divacancies. This decrease in the diffusion coefficients results from an increase in the migration barriers at low Li concentration.

Future work

With the automated statistical mechanics software tools developed during the past year, we are in a position to study the thermodynamic and kinetic properties of Li and anion insertion in a variety of electronically conducting organic crystals. During the next year, we will investigate the equilibrium voltage curve and guest ion diffusion coefficients in three candidate organic electrode materials: polyaniline, polythiophene and polypyrrole.