Back to Table of Contents

47782-AC8
The role of erosion at the head of turbidity currents - experiments and theory

M. Y. Louge, Cornell University

Introduction:

Suspension currents are ubiquitous in nature, including avalanches, sand storms and deep-sea sediment slides. They self-sustain by eroding particles from the ground, thus maintaining a density difference with the surrounding clear fluid. We investigate them with experiments and theory. Our theoretical and experimental analysis of these flows is aimed at establishing how the characteristic shape of the current's head changes with the density difference at various rates of basal erosion, which we model as an isotropic source of fluid with a different density.

Experimental Setup:

To investigate this problem we have built a new flume operating at flow speeds of 1 to 30 cm/sec, which produces Reynolds numbers of 3,000 to 90,000 large enough to replicate natural situations.

Our experiment is unique in that we inject source fluid from an isotropic injection nozzle at the base of the flume into an oncoming stream; this fixes the distance between the current's head and the source, while keeping the flow steady. The injection nozzle is especially important in that it maintains a two dimensional flow profile; this replicates the source flow analyzed in our theoretical model.

We have designed and installed and image acquisition system with camera, clean side walls and lighting that allows us to establish clearly the position of the front.

We analyze the shape and dynamics of the head under different flow conditions by varying flume inclination, source density, injection rate and speed of the uniform stream.

Recently captured photograph of the front shape for the classical Rankine problem

Theoretical Model:

We are developing a theory perturbing the classical ‘Rankine half-body' potential flow solution, which injects an inviscid source fluid onto an oncoming uniform stream.

In this problem, the absence of mixing creates a “seperatrix” streamline dividing the source and oncoming fluids.

Our theory predicts its position, as well as the streamline pattern, velocity and pressure both inside and outside of the separatrix.

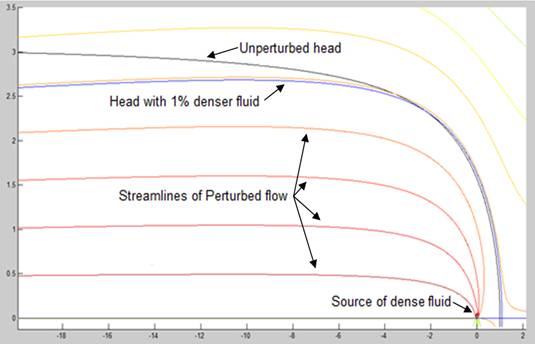
The plot outlines solution for the case where fluid of 1% higher density is injected: note that the front moves forward while the tail sinks downwards.

Head perturbation calculation

Future Work:

We are poised to carry out an experiment using a salt water solution. We will first change the density level of the incoming fluid and then adjust the slope angle of the flume between 0⁰and 5⁰. We will compare the results to our theoretical calculations. We will also investigate the role of viscosity, which creates boundary layers within the flume.

Later we will replace the salt water solution with a particle laden fluid. This will require a new injection nozzle in order for particles to enter the flume.

We are currently refining our theory by increasing the order of its accuracy. In addition we are contemplating the use of finite element software to investigate the role of viscosity and finite flume size.

Back to top