AmericanChemicalSociety.com
Reports: AC7 48337-AC7: Dynamic Anchoring of Liquid Crystals at Fluid Interfaces
Robert A. Pelcovits, Brown University
This project addresses using experimental and numerical techniques what happens when a liquid crystal is brought into contact with a flowing liquid, i.e., a situation with dynamic anchoring of the mesogenic molecules at the surface. Specifically we are studying the geometry of “driven cavity flow” with a nematic liquid crystal confined to a square well with a conventional (i.e., non-liquid crystalline) fluid flowing above. This geometry is of technological relevance, e.g., in the development of biosensors, where liquid crystals are brought into contact with a layer of phospholipid molecules or bound biomolecules such as proteins or viruses. Liquid crystal biosensors rely on optically monitoring the local nematic director changes due to the interaction of the liquid crystal molecules with the biological target. This local reorientation of the director is then amplified by the presence of long range orientational order in the nematic, and the perturbed director field is optically observed.
If the walls of the confining well are treated with a homeotropic surface alignment layer the nematic director field will necessarily exhibit a defect structure which is readily observed both experimentally and numerically. As the fluid flows we expect that the defect will be dragged by the fluid and the structure distorted. The distortion will be sensitive to both the fluid velocity and the presence of any surfactants in the fluid.
To model our problem and obtain results relevant to the time and length scales of the experimental system we are using the Lattice Boltzmann (LB) technique as applied to liquid crystals. The LB technique is a mesoscopic simulation method bridging the gap between molecular dynamics at the microscopic scale and continuum modeling approaches, and has been used to study cavity flow for single fluids. The LB technique assumes a target set of hydrodynamic equations of motion which govern the spatial and temporal variations of the nematic order parameter. There are a number of choices for the hydrodynamic equations (nematodynamics) for nematic liquid crystals. We have chosen to use the equations of Qian and Shen which have been successfully applied to interfacial problems. The nematodynamic equations consist of the momentum evolution equation for the fluid velocity and an evolution equation for the nematic order parameter tensor.
To
summarize the progress to date on the numerical simulations: the necessary
groundwork has been fully laid during the first two grant years to allow the
study of the system of interest during the final (unfunded) grant year. The
student, Pengyu Liu, supported by this grant has developed significant
expertise in liquid crystal physics, fluid mechanics and the Lattice Boltzmann
technique preparing him broadly for a future career studying complex materials
using numerical simulations. This project has also provided Pelcovits with
substantial experience in the study of liquid crystal hydrodynamics, an area he
has not previously pursued in great depth.
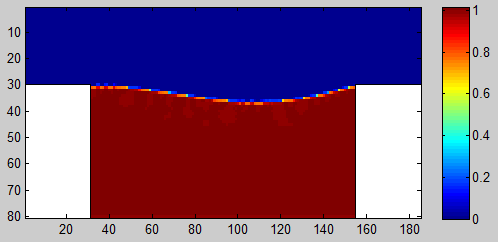 This
grant is supporting a Physics graduate student, Pengyu Liu, who is working
under Pelcovits' supervision to carry out the numerical simulations. Under
Pelcovits' guidance Liu has mastered the rather convoluted literature on
nematodynamic equations and derived the Qian-Shen equations. In the past grant
year he has developed and debugged his own LB code for the Qian-Shen system of
equations and validated this code by reproducing the LB results in the
literature for nematic viscosities. In preparation for the ultimate goal of
this project he has also developed in this past grant year a successful LB
simulation of two-dimensional “liquid-liquid” driven cavity flow, i.e., one
isotropic fluid flowing over a cavity containing a second, different, isotropic
fluid (see figure). Liu is now
preparing to bring all of these ingredients together to allow him and Pelcovits to study the
problem of interest, namely, an isotropic fluid flowing above a cavity
containing a nematic liquid crystal. The nematic director field produced by the
simulations will then be compared with experimental data using computational optical
modeling.
This
grant is supporting a Physics graduate student, Pengyu Liu, who is working
under Pelcovits' supervision to carry out the numerical simulations. Under
Pelcovits' guidance Liu has mastered the rather convoluted literature on
nematodynamic equations and derived the Qian-Shen equations. In the past grant
year he has developed and debugged his own LB code for the Qian-Shen system of
equations and validated this code by reproducing the LB results in the
literature for nematic viscosities. In preparation for the ultimate goal of
this project he has also developed in this past grant year a successful LB
simulation of two-dimensional “liquid-liquid” driven cavity flow, i.e., one
isotropic fluid flowing over a cavity containing a second, different, isotropic
fluid (see figure). Liu is now
preparing to bring all of these ingredients together to allow him and Pelcovits to study the
problem of interest, namely, an isotropic fluid flowing above a cavity
containing a nematic liquid crystal. The nematic director field produced by the
simulations will then be compared with experimental data using computational optical
modeling.
Copyright © American Chemical Society

