

43993-AC10
Multiscale Modeling of Hydrogen Embrittlement in Metals
We have carried out a crucial analysis on the recently developed self-consistent embedding quantum mechanics/molecular mechanics (QM/MM) theory of materials. The self-consistent embedding theory provides a potentially exact framework for QM/MM simulations of complex materials. We analyzed the accuracy of the embedding theory, focusing on the electronic structure of the primary quantum mechanics region. In particular, we examine the influence of embedding potential on the structural energy, local density of states, total electronic density, and electronic states at the Fermi energy of the primary quantum system. We compare the energetics and the electronic structure between the bare cluster, embedded cluster and bulk calculations in Aluminum. We find that the embedding scheme reproduces accurately the total electron density of the bulk system. The embedding method could eliminate the localized surface states at the Fermi energy that originate from the dangling bonds at the surface in the cluster calculations. Since the embedding method does not involve the electronic states from the environment, it cannot provide the correct LDOS of the system. The analysis illustrates the success and limitations of the embedding scheme in describing the electronic structure of the primary quantum region. The assessment of the embedding QM/MM method provides guidance for further development and application of the method in material problems.
 In a related project, we have developed a multiscale
method that performs quantum mechanical simulation of materials at micron scale
or beyond. The ability to perform quantum simulations of materials properties
over length scales that are relevant to experiments represents a grand
challenge in computational materials science. If one could treat multi-millions
or billions of electrons effectively
at micron scales, such first-principle quantum simulations could revolutionize
materials research and pave the way to the computational design of advanced
materials. There are two principal reasons why quantum simulations at relevant
experimental scales are important. First of all, it allows a direct comparison
between theory and experiment. For example, the rapidly emerging field of
nanotechnology demands realistic and accurate modeling of material systems at
the nanoscale. Secondly, quantum simulations at larger scales are essential
even for extended bulk crystals where periodic boundary conditions may be used.
This is due to the fact that a real bulk solid always contains lattice defects
(or impurities) whose interactions are long range - dislocations being the
prominent example. An insufficiently large periodic unit cell would lead to
unrealistically high concentrations of defects and/or impurities, rendering the
results of such simulations questionable. We have proposed a multiscale
approach that is based entirely on
density functional theory (DFT) and allows quantum simulations at the micron
scale and beyond. The method, termed QCDFT, combines the coarse graining idea
of the quasicontinuum (QC) approach and the coupling strategy of the quantum
mechanics/molecular mechanics (QM/MM) method, and represents a potentially
major advance in the quantum simulation of materials properties. Although QCDFT
is not a brute-force electronic structure method, but rather a multiscale
approach that can treat large systems - effectively up to billions of
electrons. Therefore, some of the electronic degrees of freedom are reduced to
continuum degrees of freedom in QCDFT. On the other hand, although QCDFT
utilizes the idea of QM/MM coupling, it does not involve any
classical/empirical potentials (or force fields) in the formulation - the
energy calculation of QCDFT is entirely based on orbital-free DFT (OFDFT). This
is an important feature and advantage of QCDFT, which qualifies it as a bona
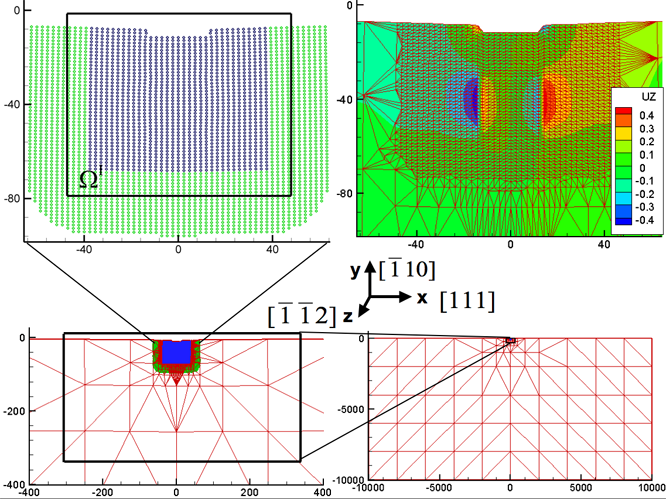
fide quantum simulation method. The figure shows an overview of the entire test
system and the relevant domain partition in a QCDFT calculation for
nanoindentation of an Al thin film. The colors indicate the out-of-plane
displacement of atoms in the z-direction. The system contains over 60 millions
atoms.
In a related project, we have developed a multiscale
method that performs quantum mechanical simulation of materials at micron scale
or beyond. The ability to perform quantum simulations of materials properties
over length scales that are relevant to experiments represents a grand
challenge in computational materials science. If one could treat multi-millions
or billions of electrons effectively
at micron scales, such first-principle quantum simulations could revolutionize
materials research and pave the way to the computational design of advanced
materials. There are two principal reasons why quantum simulations at relevant
experimental scales are important. First of all, it allows a direct comparison
between theory and experiment. For example, the rapidly emerging field of
nanotechnology demands realistic and accurate modeling of material systems at
the nanoscale. Secondly, quantum simulations at larger scales are essential
even for extended bulk crystals where periodic boundary conditions may be used.
This is due to the fact that a real bulk solid always contains lattice defects
(or impurities) whose interactions are long range - dislocations being the
prominent example. An insufficiently large periodic unit cell would lead to
unrealistically high concentrations of defects and/or impurities, rendering the
results of such simulations questionable. We have proposed a multiscale
approach that is based entirely on
density functional theory (DFT) and allows quantum simulations at the micron
scale and beyond. The method, termed QCDFT, combines the coarse graining idea
of the quasicontinuum (QC) approach and the coupling strategy of the quantum
mechanics/molecular mechanics (QM/MM) method, and represents a potentially
major advance in the quantum simulation of materials properties. Although QCDFT
is not a brute-force electronic structure method, but rather a multiscale
approach that can treat large systems - effectively up to billions of
electrons. Therefore, some of the electronic degrees of freedom are reduced to
continuum degrees of freedom in QCDFT. On the other hand, although QCDFT
utilizes the idea of QM/MM coupling, it does not involve any
classical/empirical potentials (or force fields) in the formulation - the
energy calculation of QCDFT is entirely based on orbital-free DFT (OFDFT). This
is an important feature and advantage of QCDFT, which qualifies it as a bona
fide quantum simulation method. The figure shows an overview of the entire test
system and the relevant domain partition in a QCDFT calculation for
nanoindentation of an Al thin film. The colors indicate the out-of-plane
displacement of atoms in the z-direction. The system contains over 60 millions
atoms.