Back to Table of Contents

43901-AC9
Effect of Particle Size Distribution on Drag Force in Fluid-Particle Suspensions

Sankaran Sundaresan, Princeton University

Most of the computational approaches for simulating particulate flows in industrial devices such as fluidized beds treat the suspension as a mixture of two or more inter-penetrating fluids.  The multi-fluid model equations, obtained from spatial averaging of the Navier-Stokes equations for the fluid and the Newton's equations of motion for the particles, rely on constitutive models, among which the model for fluid-particle drag is particularly important, to describe the detail of fluid-particle interactions.  While constitutive models for fluid-particle drag in fixed beds containing monodisperse and bidisperse spheres have been established [Hill et al. (2001a, 2001b), van der Hoef et al. (2005, 2007), Beetstra et al. (2007)], the drag law for general polydisperse suspensions with particle-particle relative motion have not been studied in detail.  The objective of this funded research is to use lattice-Boltzmann simulations to characterize the drag forces in low-Re bidisperse gas-solid suspensions with particle-particle relative motions, and develop drag correlations from the simulation data.

In low-Re bidisperse gas-solid suspensions, the average drag forces may be expressed as

(1)

,

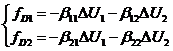where f_Di is the total fluid-particle drag per unit volume of suspension on type i particles, and ¦¤U_i is the average velocity of type i particles relative to the fluid.  The friction coefficient b_ij, owning to the linear characteristics of the low-Re flows, is a function of particle volume fraction f_i, particle size d_i, and a length scale ¦Ë on which the lubrication force between particles begins to saturate.

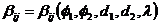
As b_ij is independent of the velocities ¦¤U_i, one can set ¦¤U₁ = 0 and ¦¤U₂ °Ù 0 to determine b₁₂ and b₂₂ from the numerically obtained drag forces f_Di, and then ¦¤U₁ °Ù 0 and ¦¤U₂ = 0 to determine b₁₁ and b₁₂.  b_ij is symmetric due to the principle of acting and reaction between the two particle species; furthermore, the row summation of b_ij yields the friction coefficients b_i = f_Di-fixed/¦¤U for bidisperse fixed beds, because Eqn. (1) must be able to recover the fixed-bed drag when ¦¤U₁ = ¦¤U₂.

We first revisited the drag in bidisperse fixed beds.  Because this problem has been studied by van der Hoef et al. (2005, 2007), it is an excellent opportunity for comparison and validation.  Moreover, accurate determination of b_i is important for the development of a general drag law for suspensions with particle-particle relative motions because of the connections between b_ij and b_i.  Our simulation data, obtained in the total volume fraction range of 0.1 < f < 0.4, with volume fraction ratio f₁:f₂ varied from 1:1 to 1:7 and particle size ratio d₁:d₂ varied from 1:1 to 1:4, agree very well with the existing data in van der Hoef et al. (2005, 2007).  The extended parameter range in our simulations enables us to confirm the deficiencies of the existing drag law.  A new drag law for fixed beds containing spheres of different sizes is proposed

(2)

,

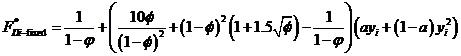where y_i is the dimensionless particle size normalized by the Sauter mean <d>

(3)

, ,

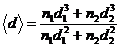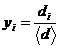with n_i the number density of type i particles, and a is given by the following cubic polynomial

	(4)

.

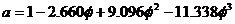The dimensionless drag force 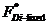 is related to b_i by

(5)

,

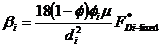where µ is the viscosity of the fluid.  This drag law, with an average error of 3.9% and maximum error of 9.4%, is more accurate than current drag laws for bidisperse fixed beds.

We then characterized the drag forces in suspensions with particle-particle relative motions.  As b_ij is symmetric and the row summation of b_ij yields b_i, it can be simplified to

,

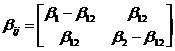where b₁₂, the off-diagonal components representing the hydrodynamic particle-particle drag, is the only free parameter to be characterized.  Our simulations show that b₁₂ is always an important contribution to the net fluid-particle drag, and can be well approximated by a linear function of the harmonic mean of b₁ and b₂

(6)

,

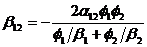where ¦Á₁₂ is a logarithmic function of the lubrication cutoff

(7)

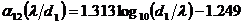 (assuming d₁ < d₂).

This logarithmic dependence indicates that the primary contribution to the hydrodynamic particle-particle drag is made by the normal lubrication force between dissimilar particles.  Eqns. (6) and (7) have an average error of 13% and a maximum error of 31%.  Both Eqns. (2-5) and Eqns. (5-6) can easily be generalized to polydisperse suspensions containing more than two particle species.  In the next year, we will extend these drag laws to suspensions with finite Reynolds numbers.

References:

1. R. J. Hill, D. L. Koch, A. J. C. Ladd, J. Fluid Mech., 448, 213, 2001.
2. R. J. Hill, D. L. Koch, A. J. C. Ladd, J. Fluid Mech., 448, 243, 2001.
3. M. A. van der Hoef, R. Beetstra, J. A. M. Kuipers, J. Fluid Mech., 528, 233, 2005.
4. R. Beetstra, M. A. van der Hoef, J. A. M. Kuipers, AIChE J., 53, 489, 2007.
5. Erratum, AIChE J., 53, 3020, 2007.

Back to top