47332-G10
Synthesis, Structural Characterization and Property Optimization of Novel Antimonides and Bismuthides Promising Materials for Thermal-to-Electric Energy Conversion
The typical Zintl phases are formed among elements with very different electronegativities and their structures can be understood by assuming a complete electron transfer from the cations to the anions. Using this approach, also referred to as the Zintl-Klemm-Bussmann (ZKB) concept, the constituent atoms can be viewed as arranging themselves in partial cationic and anionic sub-networks, all achieving closed-shells following the octet rule. In most cases this assumption is justified, especially for structures built of small, simple units. However, rationalization of the bonding in Zintl phases with complicated extended frameworks has proven non-trivial, especially in cases with extensive metal-metal interactions, which are neither typical covalent nor typical ionic bonds.
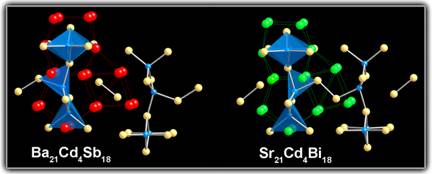
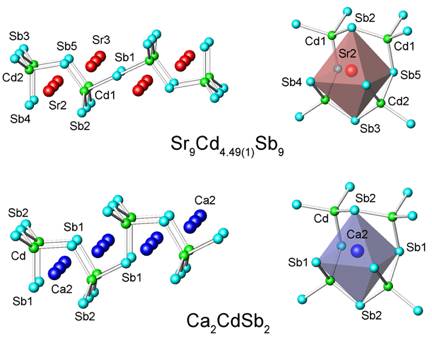
In previous studies, we have investigated Zintl-like chemistry involving d5 and d10 metals and have already reported on the structures and bonding of several ternary Zintl compounds with Mn, Zn, or Cd. A common structural element in all of these compounds are the d- metal centered tetrahedra of pnicogens, which are connected via corner or edge-sharing into larger clusters, chains, layers or frameworks. These results showed the importance of the cation-anion interactions and the delicate balance between the atomic sizes and electronic requirements in rationalizing the structures and properties. Typical examples include the structural evolution between Ca2CdSb2 and Sr2CdSb2, where the [CdSb2]4– layers in Ca2CdSb2 break into [Cd4Sb9]19– chains in Sr2CdSb2 in order to optimize the space filling with the bigger Sr2+ cations (Figure 1). Similar cation effect was recently reported for the counterparts Sr21Cd4Bi18 and Ba21Cd4Bi18. In this instance, the bigger Ba2+ cations cause the [Cd8Bi22]48– polyanions in Sr21Cd4Bi18 to break into smaller [Cd4Bi12]26– ones, which pack in a different crystallographic arrangement (Figure 2).
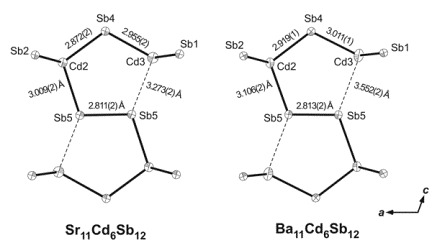
During the studies of A21Cd4Bi18 and their Sb-analogs A21Cd4Sb18 (A = Sr, Ba, Eu), a new compound was serendipitously synthesized, Ba11Cd6Sb12. The latter is isostructural with Sr11Cd6Sb12, and its structure features CdSb4 tetrahedra that share corners and form polyanionic sub-structure consisting of one-dimensional ribbons (Figure 3). Notably, there also are some short Sb–Sb bonds, which "zip" the corners of two CdSb4 tetrahedra, leading to a unique arrangement that was dubbed "double pentagonal tubes" in the original description. Applying the ZKB concept to rationalize the bonding in this structure type appears straightforward and results in the formulation [A2+]11[Cd6Sb12]22–, i.e., both Ba11Cd6Sb12 and Sr11Cd6Sb12 should be electron-precise Zintl phases. However, upon careful examination of all polyanionic interactions in the new Ba11Cd6Sb12 compound, we noticed an unusually long Cd–Sb contact, on the order of 3.55 (Figure 4). Slightly shorter, about 3.27 , but also long Cd–Sb interaction is known for Sr11Cd6Sb12. For comparison, all other Cd–Sb contacts within these units fall in the range 2.872(2)-3.009(2) in Sr11Cd6Sb12 and 2.919(1)-3.106(1) in Ba11Cd6Sb12. Such distances are comparable with the Cd–Sb distances in other intermetallic compounds with structures based on CdSb4 tetrahedra, such as Ca2CdSb2, Sr9Cd4.49Sb9, Ba21Cd4Sb18, SrCd2Sb2, etc. Based on the results from this comparative analysis, we can argue that the distance of 3.552(2) between Cd3 and Sb5 in Ba11Cd6Sb12 represents a weak interaction. Although it is difficult to quantify the strength of a given interaction according to an empirical bond-length criterium, the Cd3–Sb5 distance that is more than 20% larger than the sum of the corresponding Pauling's covalent radii clearly points out that the latter should not be treated as a typical 2-center-2-electron bond.
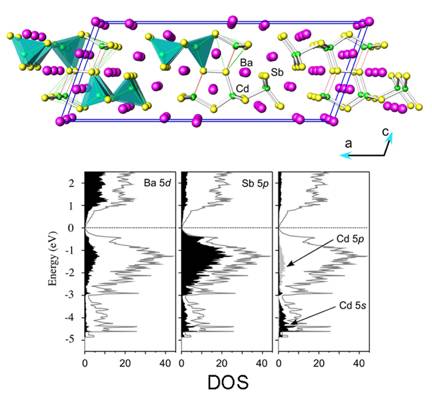
This prompted us to investigate the electronic structures of these two compounds by the Density Functional Theory (DFT) and the Local Density Approximation (LDA). Additional insights of the chemical bonding were obtained by the Extended Hckel (EH) method. Our theoretical analyses suggest that, indeed, these long Cd–Sb contacts represent weakly bonding interactions, and that the classic Zintl ideas cannot provide an adequate rationale to the bonding in these, otherwise typical Zintl phases. Following comparisons with other intermetallics with Cd–Sb polyanionic sub-networks and analyses of the chemical bonding based on our calculations, it can be suggested that the simplistic description of the "11-6-12" structure is not informative – two of the Cd–Sb interactions are very weak, while the homoatomic Sb–Sb interactions are very strong, and both are inconsistent with the notion of 2-center-2-electron bonding. Despite these subtleties, the polyanionic framework retains its Zintl-like electron requirements. A systematic examination on the electronic band structures, crystal orbital Hamilton populations and Mulliken charge populations indicates that the Sb2 dimers play important role for optimization of the bonding. These findings complement our recent reports on other related Zintl phases with transition metals, suggesting an inadequacy of the classic (empirical) rules for electron counting for understanding the complicated structures of these intermetallic compounds.
Figure 1.
Figure 2.
Figure 3.
Figure 4.