45169-AC9
Physical Foundations of the Vibratory Recovery of Residual Oil
To better predict the mobilization of oil entrapped in porous media, the process of disintegration of oil into droplets should be thoroughly understood. We have continued building such an understanding in two directions: (1) by refining the analytical models of the evolution of an oil/water interface to a complete snap-off and (2) by validating these models against computational fluid dynamics (CFD). We are now at the stage at which the analytical and computational results have closely matched each other, which attests to the correct theoretical description achieved.
Technically, this is a hydrodynamic problem of the dynamics of an interface between a non-wetting core fluid (such as oil) surrounded by a wetting annulus (water) in a constricted capillary tube. We are interested in describing the evolution of the interface toward its end configurations as the oil phase moves through pore constrictions. As established during Year 1 of the project, the geometry of the constrictions plays pivotal role in whether the oil continues to flow as a stream or disintegrates into fluid particles; the resulting state of the oil phase has fundamental significance for the methods of its recovery, including the vibratory stimulation.
The theory reported as part of the project implementation during Year 1 has now been significantly improved and validated. Whereas the earlier theory had to assume comparable thicknesses of the oil core and water annulus, as well as a much greater viscosity of the oil, the present theory is valid for arbitrary viscosities and thicknesses. Another milestone is the verification of the theory in an accurate computational-fluid-dynamics experiment.
The key elements that led to a partial-derivative equation for the evolution of the oil/water interface are as follows. In the surface-tension-driven flow, the fluids in the annulus and the core move in opposite directions, and the conservation of mass dictates that Qwater = –Qoil, where Q is the volume flow rate. The former condition means that the tangential fluid velocity at the interface is zero. With the small-slope assumption, the fluid flow in the core and the annulus can be approximated by Poiseuille flow. Combining the conservation of mass, Laplace's law for capillary pressure, and the equations for Poiseuille flow in the core and the annulus, we arrive at the evolution equation for the radial position of the interface κ(x, τ) as a function of the dimensionless axial coordinate x and time τ:
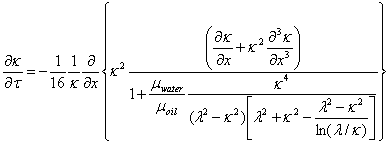 , (1)
, (1)
where μwater/μoil is the viscosity ratio, and λ(x) is the shape of the pore wall. Equation (1) is a much more general, unrestricted formulation of the quantitative interface dynamics than the simplified version reported during Year 1. Its solutions are expected to better describe the reality.
The validity of the numerical solutions of equation (1) has been verified using computational fluid dynamics. The commercial code FLUENT was used to compute the evolution of the interfaces for the same initial conditions as in the numerical solution of (1), for a variety of different scenarios.
Figure 1 shows a typical comparison between the interface shape predicted by the theory and that obtained by the fully dynamic CFD simulations. The scenario uses a sinusoidal shape of the wall; the initial oil/water interface is parallel to it. The evolution from the initial interface configuration to the break-up, obtained through numerical integration of equation (1), is shown in Figure 1, upper panel. The evolution is from the initial profile in the “back” toward the viewer; the end profile just before it snaps off is at the “front” of the plot. The formation of a large satellite drop in the neck of the constriction is predicted. The lower panel shows the same final interface shape obtained through computational fluid dynamics (water is yellow and oil is red). It is very close to the shape predicted by the evolution equation, and a satellite drop forms as well.
The close match between the theory and the CFD simulations indicates that the theoretical model correctly captures all essential features of the evolution of the oil/water interface driven by capillary forces. A correct prediction of the sizes of the oil drops forming in porous channels is an important prerequisite for the calculation of the possibility of the drops' mobilization by vibrations. The theory of the break-up can therefore be used in conjunction with the theory of vibratory stimulation to provide a complete description of the mobilization process.
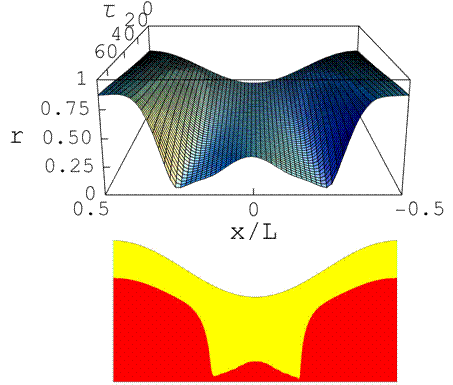
Figure 1. Oil/water interface profiles just before the break-up. Upper: numerical integration of the evolution equation, lower: computational-fluid-dynamics simulation