46779-AC10
Zeolite Structure Prediction and the Identification of Useful Synthetic Targets
There are an infinite number of hypothetical zeolite-type frameworks. However, there is only a finite number if we restrict the search to frameworks of low complexity, which we define as the number of crystallographically unique tetrahedral atoms such as silicon. A combinatorial search is performed to identify graph topologies where each silicon atom connects to exactly four neighboring silicon atoms. We apply an interatomic force field to identify topologies that can be made into a regular tetrahedral three-dimensional structure. We have identified over 5 million such structures, and the list continues to grow. About half of all newly-synthesized zeolite frameworks are already in our database.
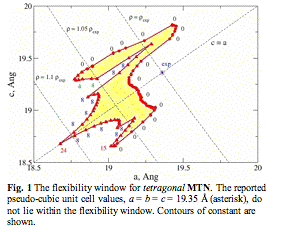
Fig. 1 The flexibility window for tetragonal MTN. The reported pseudo-cubic unit cell values, a = b = c = 19.35 Å (asterisk), do not lie within the flexibility window. Contours of constant are shown.
|
We want to identify those hypothetical
zeolites that are useful, and to assist the synthesis chemist to make the
material. To do this, we need to identify those frameworks that are likely to
be synthesized. It is not sufficient to have a low energy of formation. There
must also be a kinetic pathway to formation, which is hard to predict. We have
observed that frameworks of real zeolites exhibit a flexibility window –
a range of densities over which the framework loses rigidity. To identify the
flexibility window, we treat the framework as comprising rigid perfect SiO4
tetrahedra, which are corner-connected by hinges that allow rotations but no
stretching. Almost all of the known zeolites exhibit a flexibility window, but
many hypothetical zeolites do not. The existence of a flexibility window may
indicate a synthesizable material. One notable exception is the clathrate cubic
framework MTN. However, if we allow the material to lower its symmetry to
tetragonal (Fig. 1), a flexibility window opens up. This suggests that MTN may
be a ferroelastic material exhibiting tetragonal domains, or even domains of
lower symmetry).
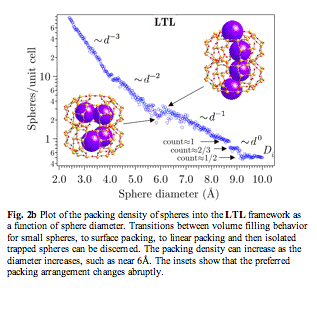
The ability of zeolites to absorb or reject molecules of a given size is important. We are seeking ways to rapidly quantify the adsorption capacities of hypothetical frameworks. Ultimately, we wish to quantify the molecular shape selectivity. Packing shapes into volumes to achieve maximum density is a surprisingly hard problem. We are examining a variant of Percus-Yevick theory to see if there is a statistical mechanics approach to obtaining the equation of state for packing shapes into zeolite pores. Meanwhile, we have implemented a direct method of packing spheres by simulated annealing. This is computationally intensive, and is not practical for analyzing a large number of hypothetical frameworks. However, the results were instructive for some of the better-known zeolite materials. An interesting example is zeolite L, or LTL framework (Fig. 2). As expected, when the sphere size is small, the slope of the packing density curve varies as the inverse cube d-3 of the sphere diameter. As the diameter increases, the slope switches to a d-2 dependence indicating that it is now surface packing. Then there is a transition to tube packing d-1, followed by flat regions where isolated spheres are trapped in cages. Eventually, the sphere size is simply too large to be accommodated by the framework. Around d=6Å, the packing density increases with diameter. This effect arises because there is a transition in the way the spheres pack. When d< 6Å, spheres nestle snugly in the side pockets of the channels, which support spheres up to diameter 6Å. Above 6Å, the side pockets can no longer support the spheres, forcing a more linear channel packing, as shown in the inset figures. This demonstrates an entropic phenomenon known as the entropic depletion force. Even though the packing density is not optimal, the spheres prefer to occupy the side pockets if they can because this increases the volume available to the other molecules in the system.
Fig. 2b Plot of the packing density of spheres into the LTL framework as a function of sphere diameter. Transitions between volume filling behavior for small spheres, to surface packing, to linear packing and then isolated trapped spheres can be discerned. The packing density can increase as the diameter increases, such as near 6Å. The insets show that the preferred packing arrangement changes abruptly.
|
Our goals for the coming year are to improve the speed of our flexibility-finding algorithm. We want to understand at a deeper level why some frameworks exhibit flexibility and others do not. We need to speed up the sorption computations significantly, and allow packing of more complicated molecular shapes. We have two promising approaches. The first is the Percus-Yevick variant (known as the replica Ornstein-Zernicke method). This will involve theory development. In addition, we will try to use a geometric computational algorithm that has been successfully used to study protein packing.
