
ACS PRF | ACS
All e-Annual Reports

41945-AC10
Noise Spectroscopy of Spin-Based and Semiconductor-Based Magnetoresistive Systems
The number of applications for magnetic sensors has grown explosively in the past two decades. In particular, the demand for small, low-power magnetic sensors has grown exponentially. Applications abound to meet the needs of users in the medical, military, information technology, and industrial communities. However, one area in which little progress has been made in recent years is small, inexpensive, low-power, low frequency sensors capable of detecting ultra-low magnetic fields. The detection of fields between a femtoTesla (10-11 Oe) to about 100 picoTesla (10-6 Oe) has been dominated by relative large, expensive, power-hungry sensors such as fluxgates, optically pumped magnetometers, and SQUIDs. If significant progress could be made in producing small, inexpensive, low-power magnetic sensors the technological impact would be great.
The most likely technology to make such progress is magnetic-tunnel-junction (MTJ) sensors combined with frequency-modulated magnetic flux concentrators to suppress 1/f noise. The recent developments that make this approach so attractive are the achievement of well over 100% values of the tunneling magnetoresistance (TMR) in MTJs, the demonstration of magnetic thin films with a saturation field of 5x10-6 Tesla, and the development magnetic flux concentrators that can operate at 104 Hz. To evaluate the combined effect of these properties, we have derived a theoretical model and incorporated it in a spreadsheet for easy evaluation of the expected performance of the sensors. The model is based on our experimental studies of noise in MTJ sensors and uses the empirical parameters for electronic and magnetic 1/f noise contributions that were obtained from our experiments.
The equation governing the minimum detectable field for a Wheatstone bridge of MTJ sensors is the following.
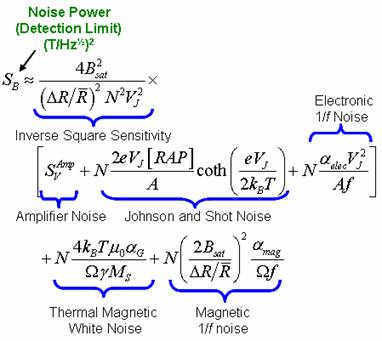 Eq. 1
Eq. 1
The parameters in Eq. 1 are as follows. SB: sensor noise power, T2/Hz; Bsat: saturation field of free layer, T; ΔR: resistance change of one MTJ from parallel to antiparallel magnetization; R: resistance of MTJ in orthogonal magnetization state; N: number of MTJ in each leg of the Wheatstone bridge; VJ: voltage drop across each MTJ; SvAmp : amplifier voltage noise power; e: electronic charge; RAP: resistance area product of each MTJ; A: area of each MTJ; kB: Boltzmann's constant; T : absolute temperature; αelec: electronic 1/f Hooge parameter; f : frequency of operation of MEMS flux concentrator; mo: permeability of free space; αG: Gilbert damping parameter; W: free-layer volume in each MTJ; g: gyromagnetic ratio for an electron; Ms: saturation magnetization of the free layer; αmag: magnetic 1/f Hooge parameter.
Equation 1 has been incorporated in a spreadsheet to enable rapid evaluation of the effect of changing the various sensor parameters. The evaluation enables rapid optimization of sensor performance. One of the most valuable aspects of the evaluation process is that it allows the user to avoid over-design in achieving some of the more difficult sensor goals. For example, it was found that the level of magnetic 1/f noise meant that TMR values in excess of 100% were so far into the regime of diminishing return as to be pointless.
The major conclusions of this work may be summarized as follows: 1) Recent advances in TMR, free-layer saturation field, and MEMS oscillating flux concentrators suggest that it may be possible to extend small, inexpensive, low-power, ultra-sensitive magnetic sensors; 2) The major challenge is to integrate these advances into sensors; 3) Our modeling has shown that there exists an unexpected new regime for magnetic sensors in which increasing the number of MTJs reduces the sensor performance. Many current designs seem to lie in this regime; 4) If successful, these sensors will play important roles in a wide range of applications including healthcare, homeland security, and national defense. Current work focuses on gaining fundamental understanding of quasi-thermal 1/f magnetization fluctuations, specifically, the extent to which these fluctuations are due to hysteresis.