Back to Table of Contents

45169-AC9
Physical Foundations of the Vibratory Recovery of Residual Oil

Igor Beresnev, Iowa State University

����������� The work during the first year has mostly focused on the studies of the surface-tension-driven break-up of non-wetting oil droplets in constricted capillaries.� This work has been submitted to refereed journals (Beresnev, 2007; Beresnev et al., 2007) (see references at the bottom).� The first article deals with understanding the general physical conditions for the break-up, while the second with the development of an accurate analytical model of the phenomenon, as the two following sections illustrate.�

Condition for the break-up of non-wetting fluids in sinusoidally constricted capillary channels

����������� This study establishes a generic geometric condition that allows or prohibits the break-up of a non-wetting fluid (oil) surrounded by water in an axisymmetric channel with sinusoidal profile.� Overlooking such a criterion has consistently been a shortcoming of previous studies.� Establishing it, on the other hand, provides a unifying framework in which results of miscellaneous published observations can be understood.�

����������� Capillary-pressure (P) distribution along the oil core in the channel is calculated using Laplace equation written in the cylindrical coordinates with axial symmetry.� The condition for the break-up of the oil in the necks of the constrictions is then written as P_neck > P_crest, where P_neck and P_crest are the capillary pressures in the necks and the �crests� of the sinusoidal profile, having the radii of r_min and r_max, respectively.� This condition, written through the geometry of the channel, becomes

λ > 2π (r_min r_max)^1/2. ����������������������������������������������������(1)

For the channel with a wavelength λ satisfying (1), the oil will spontaneously break up into isolated droplets, while, at shorter wavelengths, it will equilibrate into a cylindrical shape with constant radius.� Note that equation (1), applied to a cylindrical tube (r_min = r_max = R), reduces to the well-known condition for the Plateau-Rayleigh instability, λ > 2πR.� It thus generalizes the latter for the case of a constricted capillary.�

����������� The validity of the criterion (1) was verified in a computational-fluid-dynamics experiment using commercial code FLUENT.� Figure 1 shows the evolution of an oil ganglion, surrounded by water, in the tube geometry satisfying condition (1), illustrating the full process of choke-off.� A series of simulations were run for the values of λ bracketing its predicted threshold (1).� This simple geometric criterion was found to be correct within about 12 %, showing its surprisingly high accuracy, considering that it does not account for the dynamics of the interface.�

Quantitative dynamics of the choke-off process

����������� While criterion (1) developed by Beresnev et al. (2007) correctly prescribes the geometry sufficient for the break-up, it has been called static because it does not take the interface dynamics into account.� To make up for the lack of the dynamic description, Beresnev (2007) developed an evolution equation that provides an analytical model of the phenomenon.� The equation follows from capillary-pressure analysis in the oil phase, combined with the conservation of mass in the approximation of the �small slope� of the pore wall.�

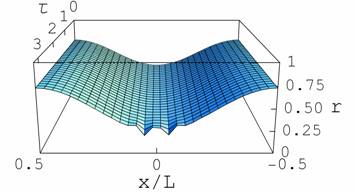
����������� For an axisymmetric capillary channel and in dimensionless variables, the radial position of the interface κ(x, τ) is described by the nonlinear equation

dκ/dτ = �(1/8κ) ∂/∂x {[κ²/2 + (μ₁/μ₂) (λ² � κ²)](dκ/dx + κ² d³κ/dx³)},������������� (2)

where x and τ are the dimensionless axial coordinate and time, respectively; λ(x) is the sinusoidal wall profile, and μ₁/μ₂ is the ratio of the oil-to-water dynamic viscosities.� The spatial variables are non-dimensionalized by r_max and time by the characteristic time scale μ₁r_max/σ, where σ is oil-water interfacial tension.��

����������� Equation 2 was solved numerically using computer package Mathematica^�.� Figure 2 presents the evolution of an interface that initially followed the wall profile, for the case in which condition (1) was satisfied.� The first time �slice� (at the rear of the plot) is the initial fluid/fluid interface.� Driven by the excess pressure in the neck, the fluid starts outflowing into the crests, which leads to the pinch-off in the neck.� The break-up in this particular example is achieved through the formation of �wavy� features on the profile.�

����������� A combination of geometric criterion (1) and an analytical tool (2) provide a complete understanding of the process of oil break-up in sinusoidally constricted channels.� With these models, the process of disintegration of oil into smaller droplets in petroleum reservoirs will be better understood.�

b

����������� Beresnev, I. A. (2007).� Dynamics of a thread of non-wetting viscous fluid surrounded by a wetting one in sinusoidally constricted capillary channels, Physical Review E (in review).�

Beresnev, I. A., W. Li, and R. D. Vigil (2007).� Condition for break-up of non-wetting fluids in sinusoidally constricted channels, Journal of Fluid Mechanics (in review).�

Figure 1.� Computational-fluid-dynamics simulation of the evolution of an oil ganglion initially filling a pore.�

Figure 2.� Evolution of a sinusoidal oil/water interface to a complete break-up.�

Back to top