www.acsprf.org

The focus of this investigation is upon establishing how flow-induced normal stresses in a particulate suspension cause boundary wear.  Of greatest interest are concentrated suspensions used for polishing purposes in abrasive flow machining. Similar suspensions in the form of cement can cause detrimental abrasive wear. The normal stress differences and particle pressure exerted by a flowing suspension have been investigated theoretically and to a lesser extent experimentally over the last three decades. We utilize this background of understanding of the rheology to address the mechanism by which combination of shear and normal stress due to particle interactions may cause boundary wear.   Of particular interest is that for these materials we can tune the imposed stress in several ways, through shear rate, particle concentration, and particle shape.  Typical particles studied for wear of hard materials are glass beads as shown in Figure 1, where 200 micron glass spheres have been used at a nominal loading of 40% by volume in a viscous liquid.  The surface damage is seen to be severe, and indicative of  chains of particles resulting from settling.   We seek to understand such phenomena from the rheological analysis of the flowing mixture.

Figure 1. Optical micrographs of glass beads used for wear studies, alongside a pristine polished Al surface and the same surface after several minutes of shear at shear rate of 12/s with 40% glass beads in glycerine. All scale bars 200 microns.

Figure 2. At left is a schematic of the flow used. At right is SEM image of paraffin wax (coated with gold before imaging) subjected to a flow (up in image) driving normal stresses 10 times the level for onset of plastic wear for 5 minutes.

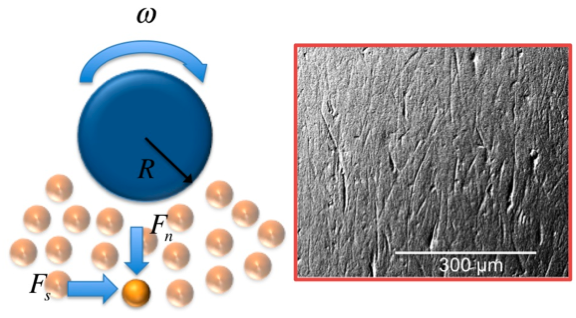The approach to the problem of determining the onset of wear has been to recognize that plastic deformation is the necessary precursor of wear.  In particulate systems, with particles of typical diameter d = 100 – 300 microns in the experimental component of this study, the scale at which the onset plastic deformation takes place is small relative to the particles.  This is due to the fact that each particle adjacent to the boundary serves effectively as an indenter to "transduce" the stress from the bulk into a force, F_n as shown in Figure 2, which is imparted on a small patch of its surface; while deformation follows elastic laws away from this scale, in a similar scale patch at the wall a plastic deformation may be imparted by modest normal forces in the bulk. By optical and scanning electron microscopy as well as profilometry, we find observable surface damage in a single pass experiment, and wear in an extended experiment, in a flowing suspension of spheres corresponds to accepted forms, e.g. Hertzian contact theory for normal stress to induce plastic deformation [1-2], based on the normal stress and the Young's modulus of the substrate (the particle is harder than the substrate by assumption).  Using the form for normal stress in a suspension, based on linearity in the shear rate and the phenomenological "normal stress viscosity" is established as proportional to the fluid viscosity [3], the onset of wear is reliably predicted for both metal (Al) and soft substrates (e..g. paraffin wax). The latter are quite useful for establishing that contacting networks of particles are not essential for the wear as wear can be induced in density-matched suspensions of smooth spheres at 40% volume fraction, as illustrated by Figure 2, showing a schematic of the wear test and the surface damage at a shear rate (and hence normal stress) of about 10 times the onset stress.    Unlike the case of the glass beads in Figure 1, neither settling nor rising occurs for this flowing mixture, and thus we have a well-controlled experiment.

To develop further theoretical understanding of the normal stresses, particularly for smaller-particle systems, we have continued to develop the microstructural understanding of these materials, considering both simple shear and complex (e.g. contraction) geometries.  Combining experimental study in collaborative efforts with our own discrete-particle simulations, we have shown that the near-wall microstructure is severely distorted, thus leading to the necessary microscale arrangement to induce strong normal stresses in the flowing material.  These stresses must be continuous at the boundary and this mechanical continuity is what provides the connection allowing prediction of onset of wear. 

Less theoretically well-founded than onset of wear is the analysis of rate of wear.  Nonetheless, there is no reason that the phenomena driving wear need to be expanded. We are proceeding to develop the expression for wear rate based on the ideas noted above. The theory for the normal stresses does not need alteration, as experiments show the normal stress differences of crushed and spherical particles, but divergence takes place at lower solid fraction.   There are two primary questions addressed by this work, which is proceeding primarily by experiment: 1) what is the form of wear particle formed? and 2) is surface rearrangement (deformation of asperities, for example) a primary mechanism for smoothing perceived as polishing? These are particularly of interest for spherical particles. Proceeding to particles with sharp edges (acicular particles), analysis of sharp indenters combined with our understanding of the normal stresses imparted indicates that wear particle formation is likely to be orders of magnitude more efficient, with stresses necessary for the onset of wear also significantly reduced.  Perhaps the most challenging aspect of this work is to parametrize the particle shape and thereby develop a way to characterize a sample.  We also perform atomistic molecular dynamics simulation in collaboration with colleague J. Koplik (CCNY Physics) to assess the molecular mechanism of onset of plastic deformation in metallic substrates.  

1. V.K. Gorona, V.K. Jain, G.K. Lal 2006 Wear 260, 128.

2. K. L. Johnson 1985 Contact Mechanics. Cambridge University Press.

3. J. F. Morris, F. Boulay 1999 J. Rheol. 43, 1213.