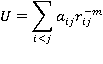www.acsprf.org

This report describes work that we have done in the past year to understand dynamic properties of liquids using a novel coarse-graining approach. The past several decades have created a striking picture of liquid-phase dynamic properties—like self-diffusivity and viscosity—as being shaped and predicted by static structural and thermodynamic quantities. This body of work includes the early free volume theories of liquids and more recent efforts that express dynamic transport coefficients as unique functions of excess or configurational entropy. These ideas are suggestive that simple model systems of particles with repulsive interactions are sufficient to predict kinetic properties in a wide range of more complex ones, provided the latter can be mapped appropriately. Indeed soft sphere models (particles with an inverse-power repulsion) have been shown to be able to predict the density- and temperature-scaling of diffusion coefficients and other relaxation times in simple liquids, mixtures, and polymers. For soft spheres, all state properties are a unique function of a single reduced thermodynamic variable ρ^m⁄3T^-1 where m is the repulsive exponent, and several groups have shown that effective soft sphere exponents can be be found for many systems that cast kinetic coefficients in this scaling.

Our work has suggested that the repulsive perspective picture of dynamics can be generalized by a suitable mapping of arbitrary systems to reference soft-sphere models. We have taken a novel approach to this task using a coarse-graining theory developed in our group. Namely, we use a quantity called the relative entropy to quantify the phase-space overlap that a putative “coarse-grained” soft sphere system has with a real system exhibiting more complex interactions (e.g., attractions). The relative entropy, broadly, measures the information lost upon coarse-graining and we have previously demonstrated that its minimization can be used to design accurate coarse models of a number of systems. Based on this idea, we developed simulation algorithms that convert reference simulations of a given system into an appropriate soft-sphere model and that compute the corresponding (minimal) value of the relative entropy, which serves as a “score” for the fitness the soft-sphere model. If the soft-sphere interaction potential is written as

where a_ij and m are constants and r_ij is the distance between particles i and j, then these algorithms give effective constants a and m.

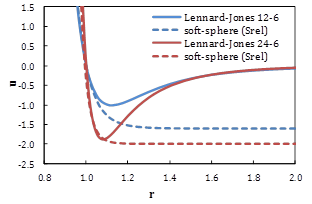
In the past year, our tests of this approach have been applied to well-studied models of binary glass-forming systems consisting of size- and energy-asymmetric particles interacting through Lennard-Jones-like potentials of varying repulsive exponent. Importantly, we have shown that relative entropy minimization is able to extract effective soft-sphere exponents that collapse simulation diffusion coefficients according to soft-sphere scaling (Figs. 1-2). This is particularly interesting in comparison with the recent picture of Dyre and co-workers that uses pressure-energy correlations to extract effective soft-sphere scaling; in contrast, the relative entropy approach matches a distinct set of interparticle correlations. The fact that latter-determined average exponent is in close agreement with the pressure-energy picture suggests either an insensitivity to the exact value of the exponent or a deeper relationship born out in constraints that repulsive interactions place on the multidimensional potential energy landscape.

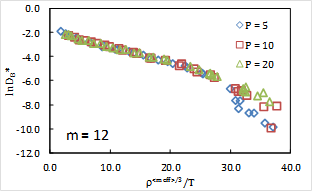
We have also found that the relative entropy predicts how the effective soft-sphere scaling exponent changes with temperature and pressure (Fig. 3). It decreases with increasing pressure, approaching that of the original Lennard-Jones system, which is consistent with the diminished role of attractions at high densities. Interestingly, however, it also decreases as the temperature is lowered, where particles appear “softer”. Since such behavior is not expected when cooling at constant density, this indicates that the density changes with constant-pressure cooling are the dominant determinant of the exponent. Indeed, our results show a much greater sensitivity of the exponent to pressure/density than temperature. An important implication is the existence of a maximum effective exponent at higher temperatures, where particles are “hardest” and which thermodynamic arguments show must exist where the usual and constant-exponent expansion coefficients are equal.

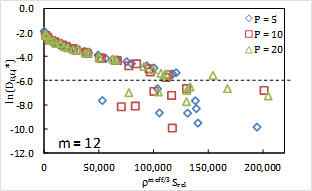
The value of the relative entropy itself in these calculations provides a new perspective. Once effective soft-sphere exponents are determined, we compute these using modern free energy algorithms. Remarkably, we find that the diffusion coefficient scales in a predictable way (near linearly) with the density-scaled value of the relative entropy (Fig. 4). The correspondence holds at least until the diffusion constant reaches very small values, in the deeply supercooled regime, where statistical errors preclude further analysis. Importantly, the scaling is determined entirely from the relative entropy analysis. This gives a predictive approach to dynamics, but moreover, the emergence of the relative entropy in this context potentially provides an natural, “coarse-grained” interpretation of entropy-based pictures of liquid dynamics.

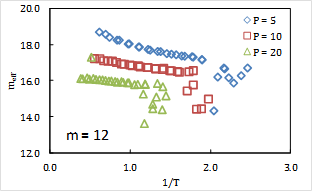
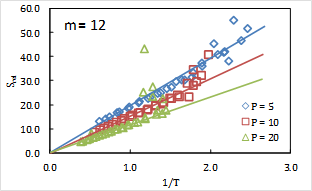
Further investigation shows that the relative entropy scales almost perfectly linearly with inverse temperature, for many different pressures (Fig. 5). This finding is surprising because a first-order cumulant expansion of the relative entropy suggests the emergence of this kind of behavior only at very high temperatures. That this correlation persists to low liquid temperatures—coupled with the ability of the relative entropy to predict diffusion constants—suggests a very powerful strategy for fluid state models. Namely, that simpler high-T perturbation theories of liquids can be used to predict dynamic properties across a huge range of state conditions, through the relative entropy route. Ultimately, these efforts are seeking a new “corresponding-states” theory of dynamics based on an underlying soft-sphere model, that we are continuing to test with a greater variety of model systems.