www.acsprf.org

We have hypothesized that aromatic hydrocarbons in crude oil can liberate calcium ions from chalk minerals. With the liberated calcium ions, aromatic hydrocarbon molecules form hydrophobic nanostructures that determine the pore wettability of carbonate oil reserves. Here we show spectroscopic evidence that there are strong interactions between the model calcite (CaCO₃) surface and aromatic hydrocarbons including benzene (C₆H₆), toluene (C₆H₅-CH₃), and ethylbenzene (C₆H₅-C₂H₅) (BTE).

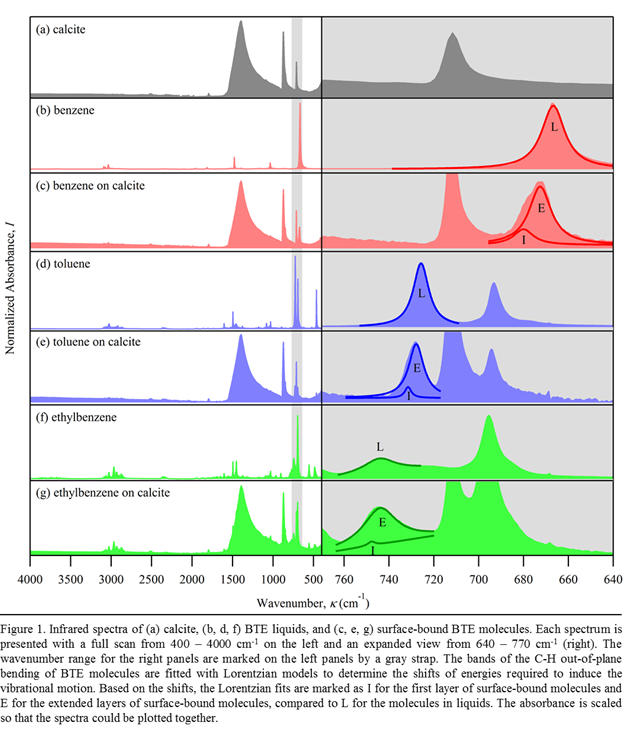
To probe molecular interactions at calcite-BTE interfaces, we mixed 100-mL dehydrated benzene, toluene, or ethylbenzene with 400-mg single-crystal calcite gains, which have diameters between 45 to 53 µm and a total surface area of 0.600(±0.006) m² g^-1. By this procedure, we obtained calcite grains that are coated with several hundred layers of BTE molecules. We placed the grains on the sample stage of an attenuated total reflectance (ATR) Fourier transform infrared spectrometer (FTIR). As the BTE molecules evaporate from the grain surfaces into air, we measured the absorption of light with wavenumbers from 400 to 4000 cm^-1 by the mineral-liquid interface.

The thickness of the adsorption layers kept decreasing as BTE molecules evaporated. When the layer became thin enough, the absorption of light by the first BTE layer became distinguishable from the extended layers, as shown in Fig. 1. Four of the spectra were obtained with pure calcite (a), benzene (b), toluene (d), and ethylbenzene (f) as controls. The comparison among them reveals that the infrared (IR) region from 640 to 780 cm^-1 contains vibrational bands distinctive for each compound. This region is highlighted by the gray band in the left panels of Fig. 1 and expanded in right panels. In the right panels, liquid (L) and surface-bound benzene molecules are shown to have signature bands at 640 – 690 cm^-1 (b and c), liquid and surface-bound toluene at 720 – 740 cm^-1 (d and e), and liquid and surface-bound ethylbenzene at 730 – 760 cm^-1 (f and g). These bands correspond to the synchronized out-of-plane bending of aromatic C-H bonds. The comparison of these liquid and surface-bound IR bands shows that in the presence of the calcite surface, the center of the bands are shifted to greater wavenumbers, suggesting that higher excitation energies are needed to induce the bending motion (E = , where E is the energy, c is the speed of light and is the reduced Planck constant). Moreover, the absorption bands for surface-bound BTE molecules consist of shoulder regions with wavenumbers greater than the centers. We interpret this splitting of the C-H bands as a result of different interactions that BTE molecules experience with the surface. The shoulder is thus created by an interaction of the first (I) molecular layer with the surface, which is stronger than the extended (E) layers. We fit the surface-bound IR absorption with Lorentzian functions. The centers of the L, I, E bands are summarized in Table 1 for different BTE molecules.

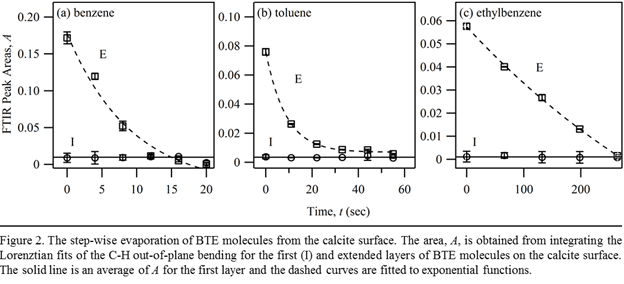
The separation of the C-H bands between the first and extended layers of surface-bound BTE molecules is also supported by the changes of their absorption intensities as evaporation progresses. As shown in Fig. 2, for all three aromatic hydrocarbons, evaporation reduces the absorption intensities for the extended layers reduce exponentially with time while the intensities of the first layers remain constant.

We interpret the strong interactions between the calcite surface and the first layers of BTE molecules as cation-p interactions. The cation-π interaction arises from the electrostatic force between a positively charged ion and the permanent quadrupole moment of a neutral molecule.

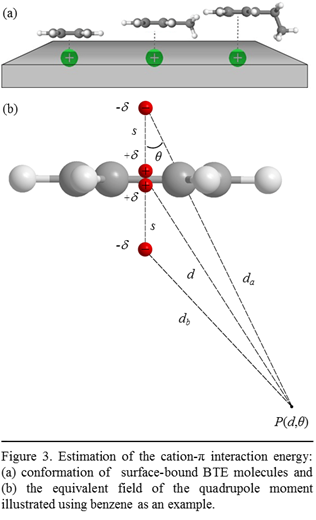
We now compute the cation-p interactions between the calcite surface and the BTE molecules using a semi-classical approach. In our computation, we place the BTE molecules with their aromatic plane in parallel with the calcite surface, as shown in Fig. 3a. We make this simplification based on our observation that except the synchronized out-of-plane bending of aromatic C-H bonds, there is no discernable shift (i.e., > 1 cm^-1) for any of the other vibrational motions measured in the range of 400 – 4000 cm^-1. For example, benzene molecules have five other vibrational motions including the three C-H stretching modes centered at 3091, 3071, and 3036 cm^-1, the C–C stretching at 1478 cm^-1, and the C-H in-plane bending at 1035 cm^-1, all of which are movements with in the aromatic plane. The lack of disturbance to all the in-plane vibrational motions and the presence of shifts for the out-of-plane motions support the parallel configuration.

In the direction perpendicular the aromatic plane, we approximate the quadruple moments of BTE molecules as two positive and two negative charges arranged to create two opposite dipoles, as shown in Fig. 3b, the potential field of the quadrupole is:

where the quadruple moment Q = -2ds², ε₀ = 8.85×10^-12 C² J^-1 m^-1, d is the distance from the testing point P to the center of the aromatic ring, and q is angle formed by the line connecting P and the ring center and the z axis. We further assume that the surface calcium cations are located underneath the center of the aromatic ring (i.e., q = 0). This gives the energy of the cation-p interaction to be:

where q is the charge of the surface calcium cation. Because each calcium ion has six bonds in calcite, the nominal charge of surface cations is:

where e = 1.6x10^-19 C. Combining the above equations gives

.

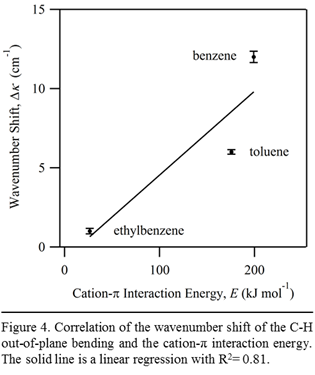
The values of Q for BTE molecules can be obtained from the literature. We estimate the values of d by performing density functional theory (DFT) optimization of calcium-BTE complexes. The calculated energies of cation-p interactions correlate well with the IR shift for the first layers of BTE molecules on calcite, as shown in Fig. 4.

Table 1. Wavenumber Shifts of Synchronized Out-Of-Plane Bending for Aromatic C-H Bonds