www.acsprf.org

49545-ND9:

Closed-Loop Reservoir Management Using an Accelerated Karhunen-Loeve-Galerkin Model in a Model-Predictive Control Framework

Karlene A. Hoo, Texas Tech University

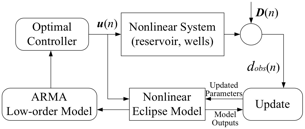
           The underlying goal of this project was to establish fundamental conditions for closed-loop stability for a particular optimum closed-loop management framework of an oil producing reservoir and its wells (Fig. 1). This management framework contains a computational model of the complex, nonlinear reservoir and wells that the optimizer uses to decide on how much water is injected to maximize net present value (NPV).  Note that we have abandoned the Karhunen-Loeve-Galerkin (KLG) model in favor of a control-relevant model more suitable for closed-loop stability analysis. The computational model is an approximation of the real system; however, the significant characteristics of the real system also is not known due to the complex geology and difficulties associated with obtaining accurate, timely and cost-effective measurements of sensitive process variables and parameters.  In almost all situations, historical databases are mined and reasonable assumptions are made to facilitate model development and model parameter estimation.

Fig 1: Schematic of closed-loop management framework.

Commercial computational software that simulates oil production in a reservoir exists (Schlumberger'sECLIPSE) and can be used as a surrogate for the real system.  Simulated or in silico data can be used in conjunction with history data to identify a suitable model for model-based control applications (such as the one studied here) and for model parameter estimation and updates.  Updating the model parameters enables the model's predictions to remain close to the actual measured values.  Unlike related chemical systems whose time responses are on the order of minutes and seconds, time responses associated with a reservoir is usually on the order of days. This is a mixed blessing. On the one hand there is time to calculate a regulation decision; on the other hand, the results of a regulation decision takes days to verify the outcome.  Another major difference is that while an analysis of closed-loop stability of a chemical system can be assured with a suitable linear model because the system is operated around the designed nominal conditions; no such counterpart exists for these reservoirs.  Hence, model parameter updating and even model substitution are necessary.

Initially, we worked with a two-phase reservoir model developed in MatLab. Later, the ECLIPSE environment was learned and then PETREL.  Reliability of the TTU computer network to execute ECLIPSE and PETREL remains an issue.  We identified two parameters, porosity and permeabilty, that contribute significantly to model/plant mismatch.  Later in our studies, we abandoned the KLG model and researched a nonlinear autoregressive with exogenous (NLARX) inputs model with model parameter updating. The resulting updated model is used to identify an approximate linear model to be used to improve NPV in the management framework.

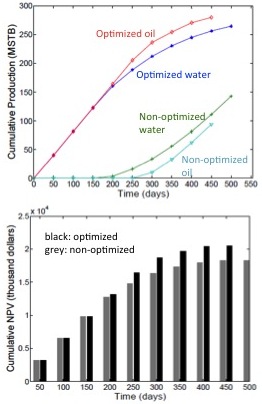
Fig 2: Top Cumulative production. Bottom: Cumulative NPV.

            Stability of the closed-loop system with a linear model is well established. This is not the case for the general nonlinear model.  Since the nonlinear model may lead to convergence issues, it is not unusual to replace it with a reduced-order model (ROM). The type we identificed is the NLARX.

           Primary contributions: 1) A Markov chain Monte Carlo (MCMC) approach is embedded in the closed-loop reservoir management framework. 2) A formal stability theorem of a nonlinear closed-loop system was established and proven based on the circle criterion.  Using a two-phase two-dimensional oil producing reservoir model in a 5-spot pattern (81 grids), 4 NLARX models are identified (5 wells the reservoir is divided into four parts, each containing a water injection well and a pseudo oil producing well) and used to demonstrate the closed-loop stability theorem.  Each grid in the reservoir is assumed to have uncertain values of porosity and permeability.  NLARX models are identified (one for each spot, each containing a water injection well and a pseudo oil producing well) and used to demonstrate the closed-loop stability theorem.  Each grid/spot in the reservoir is assumed to have uncertain values of porosity and permeability.

Figure 2 shows the oil and water production and the NPV with parameter updating and closed-loop optimal management at each control step (unit of days).  The stability of the nonlinear model-based closed-loop system was established using the circle criterion and a suitable Lyapunov function based on the following assumptions:

A(1): the p×p matrix Z(s) = I+KC(sI+A)^-1Bis strictly positive real.

A(2): There exists a mapping h satisfying F(x,u) = P^-1C^Th (x,u)

A(3): There exists a nonnegative continuous function ρ(á) such that ||h(x,u) ||₂ ²ρ(y)

A(4): There exists a nonnegative function ρ₀(á) such that ρ(y) ²ρ₀(y) ||y||₂with ρ₀(y) < (2k-λ_min(K))²/4, where λ_min(K) is the minimum eigenvalue of a symmetric positive-definite matrix K and k is the Lipschitz constant.

It then follows that there exists a function a(.) such that the closed-loop system is globally exponentially stable.

Theorem: Consider the nonlinear system: dx/dt = Ax + Bu + F(x,u) with measurement: y = Cx + Du. The nonlinear system is assumed controllable and observable and A is Hurwitz.  All nonlinearities are expressed by F(.,.).  Assume that (A1)-(A4) are satisfied.  Then there exists a function a(y) such that the closed-loop system is globally exponentially stable.

The NLARX models were identified from the added water rates and the produced oil and water rates.  Each NLARX model satisfied A(1) to A(4) and thus the theorem.  Therefore, the nonlinear closed-loop system represented by the NLARX model is globally exponentially stable.