www.acsprf.org

Stochastic splitting method improves efficiency of polymer dynamics simulations

Many polymer dynamics simulations of entangled polymer melts and solutions are built on numerical solutions of the Rouse model.  For example, "sliplink" models — developed to represent entangled polymer dynamics, in which reptation, contour-length fluctuations, and constraint release emerge naturally — spend most of their time describing the wiggling of the Rouse chain that threads the sliplinks.

It turns out there are more efficient ways of generating future configurations of a fluctuating Rouse chain, than by numerically integrating the Rouse equation with noise, as is commonly done.  Because the Rouse equation is linear, it can be formally solved in terms of the noise history.  This allows chain configurations to be generated at arbitrary future times.  This result holds even in shear or extensional flow. 

In practical applications, not all of the time evolution can be solved exactly.  For example, in a sliplink simulation, affine motion of sliplinks in flow cannot be incorporated into the exact solution.  This motion is best described in real space, while the Rouse solution is carried out in Rouse (arclength Fourier) modes.

To deal with this situation, we have developed a technique of stochastic operator splitting.  It is related to methods for deterministic PDEs such as the alternating direction implicit (ADI) method for time-dependent diffusion in multiple space dimensions.  The idea is to split the time evolution into a part exactly solvable in Rouse modes, and another part best handled in real space.  Then we alternate timesteps with the two operators.

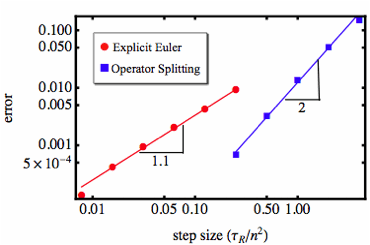
Figure 1.  Weak convergence of stochastic Euler (red) and splitting (blue), error versus step size.

We can analyze how the splitting solution approaches the exact solution as the timestep decreases.  Typically we are interested in weak convergence — accurate calculation of quantities when averaged over the noise.

We have compared our method to the usual stochastic Euler method for a Rouse chain with nonlinear springs in shear flow.  The Euler method converges with weak order 1, while our new method is weak order 2.

Our stochastic splitting method also displays greatly improved stability:  even with large timesteps, deviations from the exact trajectory are bounded, and confined to short wavelength modes of the chain.  This behavior is reminiscent of the deterministic Crank-Nicholson or ADI methods, and arises from the exact treatment for high-derivative operators in our method.

Our stochastic splitting method is generalizable to a wide variety of spatially varying order parameters, evolving under combined action of noise, linear and nonlinear forcing, and flow.

Isoconfigurational averaging reveals the tube in entangled polymer melts

Modern theories of entangled polymer dynamics rely on the concept of a "tube", which replaces the uncrossability constraints on a given chain arising from nearby chains, with a confining "tube potential".  The centerline of the tube is called the primitive path. 

The tube diameter a sets the scale over which a chain can wander transversely from the primitive path before nearby uncrossable chains impede its motion.  The entanglement length Ne is the arclength of a chain strand of dimension a.  The tube diameter and monomeric friction factor are the two "microscopic" parameters in the successful modern theory of flow of entangled polymer melts.  However, the tube is difficult to "image" directly in experiments.  Thus attempts have been made to "see" the tube in simulations. 

Prior to our work, the main approach to visualize the tube in simulations has been various "chain-shrinking" methods, in which the free ends of chains in the system are fixed, and the tension along the chains increased until each chain becomes a set of straight segments between pairwise contacts with other chains.  The primitive path is approximated as the stepwise linear path, and Ne as the number of monomers between contacts.

Chain-shrinking methods are limited because of the "damage" done to the chain conformations by the shrinking process.  We would prefer to observe the tube simply by watching the chains fluctuate with no external forces applied.  To do this, we turn to an earlier approach of simply averaging the chain trajectory over a short time Ta, long enough for an entanglement strand to explore the tube but short compared to timescales for stress relaxation.  The time-averaged chain path approximates the primitive path.

We greatly improve the statistics of this method with isoconfigurational averaging:  from the same starting configuration, we make many short movies of the subsequent chain motion, each with different random initial velocities.  We average not only over where the monomers of a given chain wandered in one short movie, but a cloud of points where each monomer traveled in many different movies. 

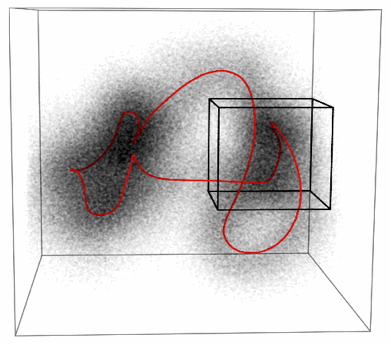
The resulting primitive path is a smooth curve, with a persistence length of about Ne/2.  Because we do not shrink the chains, we can determine the tube confining harmonic potential, quantify how the tube diameter varies along the chains, and measure how the tube broadens near a free surface (where missing entanglements reduce chain confinement).

Figure 2.  "Cloud" of monomer positions and primitive path (red) for a polymer melt consisting of a single self-entangled ring in 3d periodic boundary conditions.  (System box is dark cube.)

For these studies, we prefer to simulate a melt of a few long entangled ring polymers.  Long rings are a proxy for a melt of long entangled chains, but have no free ends.  With rings, entanglement is permanent, which is ideal for watching chains fluctuate in their tubes. 

Of course, we must first "topologically equilibrate" the melt of rings, by allowing the chains to cross occasionally.  We verify equilibrium by watching the ring conformations fluctuate, then turn off chain crossing to observe the tube. 

We are currently using isoconfigurational averaging to explore the effects of 1) deformations of the melt (uniaxial extension and compression), and 2) tension applied to linear chains.  At issue is the question, relevant to modern theories of nonlinear rheology of entangled polymers:  what are the properties of the tube for chains that have been stretched or aligned by flow?