www.acsprf.org
Reports: ND649010-ND6: Pattern Formation in Spatially Structured Active Media: Theory and Simulations
Bulbul Chakraborty, PhD , Brandeis University
We have achieved a numberof new results on the behavior of repulsively coupled chemical oscillators, andmade significant progress in developing a framework for stochastic differentialequations that model reaction-diffusion systems.
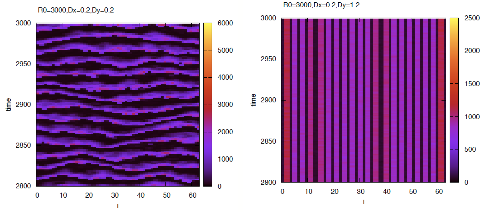
| Fig 1: (Top) Frequency order parameter and bifurcation diagram illustrating phase synchronization with increasing K. (Bottom) (a) The different helicity patterns, (b) Domains of different helicities (white and green). The red region shows the oscillators that are synchronized. |
 Coupled Chemical Oscillators: Westudied a minimal model of theexperimental system studied in the Fraden- Epstein group (J. Phys. Chem.Lett. 1, 1241-1246 (2010)). The model captures the geometricalfrustration that arises in oscillators preferring to be p out of phase but are placed on a lattice on which that patterncannot be achieved globally, for example, on a hexagonal array. We numericallysolved the differential equations arising from phase oscillators with random(Gaussian-distributed) frequencies, coupled repulsively through nearest neighbor interactions on a 1D chain,1D ring, and on a 2D hexagonal array. The most interesting results are obtained on a triangular lattice.
Coupled Chemical Oscillators: Westudied a minimal model of theexperimental system studied in the Fraden- Epstein group (J. Phys. Chem.Lett. 1, 1241-1246 (2010)). The model captures the geometricalfrustration that arises in oscillators preferring to be p out of phase but are placed on a lattice on which that patterncannot be achieved globally, for example, on a hexagonal array. We numericallysolved the differential equations arising from phase oscillators with random(Gaussian-distributed) frequencies, coupled repulsively through nearest neighbor interactions on a 1D chain,1D ring, and on a 2D hexagonal array. The most interesting results are obtained on a triangular lattice.Patterns on a Triangular Lattice: On a triangular lattice, the optimallocal pattern of nearest-neighbor oscillators locking into a p phase difference is incompatible with thegeometry. Results from ournumerical simulations show that the frequencies synchronize beyond a criticalcoupling strength (for a finite size system), however the phase pattern remainsdisordered with domains of different helicities frozen in (Fig. 1). Experimentsperformed in the Fraden group show clear patterns of domains with differenthelicities, and the structures are qualitatively similar to our numerical results. The experimental system, however, has acoupling that is quite different from the sine function in the Kuramotomodel. Specifically, the effectivecoupling, measured experimentally, is always positive and can be modeled as aquadratic function cutoff at 2p. We are now extending ournumerical studies to analyze domain formation in oscillators that are locallycoupled through this purely positive interaction.
Lattice Models of Reaction-Diffusion Systems: Theoretical studies of chemical oscillations broadlyfall into two categories: (1) a rate equation approach in which the reactantsare assumed to be well mixed, and (2) a partial differential equation approachin which spatial dependence is taken into account by adding diffusion terms tothe rate equations. These two approaches qualitatively explain experimentalmost of the phenomena observed in the microfluidic droplets. It is, however, known fromtheoretical studies of individual level models of reaction diffusion systems(Butler and Goldenfeld, Phys. Rev. E 80, 030902 (R) (2009)) in the context ofpopulation dynamics, that the intrinsic noise in these systems can change thephase diagram, and enhance pattern formation. The parameter that controls the fluctuations is the volumeof a well-mixed patch. This volumecan be estimated as![]() , where D is a typical diffusion constant, R is a typicalreaction rate and d is the spatial dimension of the system. This parameter can be controlled in theBZ microfluidic array tuning the concentration of the reactants. We have initiated a study of aone-dimensional lattice in which each site has chemical reactions correspondingto a single Brusselator, and the activator and inhibitor can hop from one latticesite to another with specified diffusion rates.
, where D is a typical diffusion constant, R is a typicalreaction rate and d is the spatial dimension of the system. This parameter can be controlled in theBZ microfluidic array tuning the concentration of the reactants. We have initiated a study of aone-dimensional lattice in which each site has chemical reactions correspondingto a single Brusselator, and the activator and inhibitor can hop from one latticesite to another with specified diffusion rates.
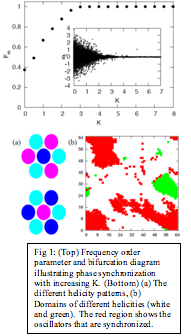
| Fig 2: (Left) Power Spectrum in the mean-field fixed-point regime. The clear peak at finite frequency indicates coherent oscillations (Right) (a) Limit cycle corresponding to the same parameters as the left figure.
|
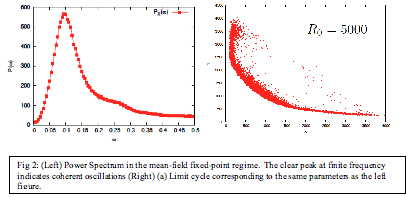
| Fig 3: Phase diagram of the mean-field 1D Brusselator model. The vertical axis represents the ratio of the diffusion constants of the inhibitor and the activator species and the horizontal axis represents the creation rate of the activator. |
 Resultsfrom a single stochastic Brusselator: Beforestudying the spatially extended model, we analyzed the phase diagram of asingle stochastic Brusselator. Inagreement with previous work on this model (Boland et al, J. Stat. Mech, P09001(2008)), we find that in the fixed-point regime of the meanfield model, thestochastic system exhibits amplified coherent oscillations as demonstrated bythe power spectrum shown in Fig. 2. Noise, thus, induces oscillations with a noisy limit cycle in the fixed-pointregime of the mean-field (deterministic differential) equations.
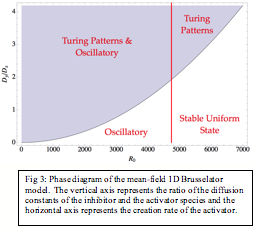
Resultsfrom a single stochastic Brusselator: Beforestudying the spatially extended model, we analyzed the phase diagram of asingle stochastic Brusselator. Inagreement with previous work on this model (Boland et al, J. Stat. Mech, P09001(2008)), we find that in the fixed-point regime of the meanfield model, thestochastic system exhibits amplified coherent oscillations as demonstrated bythe power spectrum shown in Fig. 2. Noise, thus, induces oscillations with a noisy limit cycle in the fixed-pointregime of the mean-field (deterministic differential) equations. Results from a 1D lattice of stochastic Brusselators: Fig. 3 shows the mean-field phase diagram of aone-dimensional Brusselator model with the inhibitory species represented by y and the activator species represented by x. Therate R0 in Fig. 3 represents the creation rate of theactivator. We studied thestochastic model over a range of parameters. Fig. 4 shows space-time plots at R0 = 3000, and Dy/Dxvarying from 1 to 6. There is a clear signature of emergenceof Turing patterns in the mean-field turing-oscillatory regime. Even at Dy/Dx =1, the space-time plot shows clear deviations from a pure oscillatorybehavior. We are in the process ofcarefully analyzing the pattern formation in the one-dimensional stochasticmodel. In addition, we haveinitiated studies of an inhomogeneous lattice that is meant to model the BZmicrofluidic array. In this lattersystem, the diffusion constants are different in different parts of the latticethat represent the oil and water regions. Preliminary results show an even richer phase diagram of the stochasticmodel in this spatially structured medium.
Field Theory of the Stochastic Brusslelator: Stochastic models can berepresented by field theories using operators that correspond to the processes(reaction and diffusion) occurring in these models (U. C. Tauber et al, J.Phys. A 38, R79 (2005)). We have constructed a field theory for the stochasticBrusselator model, and in collaboration with Rajesh Ravindran from theMathematical Sciences Institute in India, we are in the process of analyzingthis field theory. One of our aimsis to characterize the phase transitions in these non-equilibrium systems.