www.acsprf.org

From properties to structure: new strategy for modeling amorphous catalysts and supports

Ab initio models have been successful in the past to model zeolites[1–4] and metal surfaces including kink sites and dopant sites. However, important amorphous supports like silica-alumina and amorphous silica have not been amenable to ab initio modeling without ad hoc assumptions about the support structure. Nevertheless, some have attempted to model catalysis on amorphous supports. Examples include the molybdena-silica catalyst for olefin metathesis,[5] isolated vanadate sites supported on MCM-48 for partial oxidation,[6] and olefin metathesis by methyltrioxorhenium on amorphous silica-alumina (SA).[7, 8] We have developed a systematic ab initio method to model active sites on amorphous materials. We use new constrained optimization techniques to enable systematic computational studies of catalysis and absorption on amorphous supports.

The typical strategy for modeling crystalline supports is to compute the chemical properties from models which are constructed based on known structural information. This strategy has also been used to model amorphous catalysts and supports. However, for amorphous catalysts and supports little structural information is known a priori. Instead, we will start with the chemical property of interest and then compute the lowest energy structure having the desired property. Our computational framework is based on the following four postulates:

(1)     Amorphous supports are solids so peripheral atoms in a cluster model

should be immobile – not allowed to move during the chemical process.

This is the same as the procedure commonly used to model catalysis in

zeolites with cluster models.

(2)     Peripheral atom positions influence chemical properties of the site.  Sites

with peripheral atoms fixed in different configurations will have different properties.

(3)     Peripheral atoms can be arranged in continuous distribution of positions. 

This differs from models of zeolites, where peripheral atom positions are taken from a discrete list of crystallographic positions.

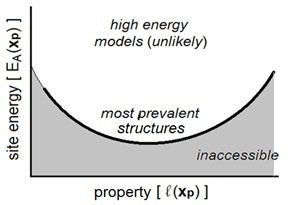
(4)     Low energy sites are more prevalent than high energy sites. While amorphous

materials are not equilibrium structures, they are not likely to be extremely far from equilibrium so we expect high energy sites to be rare.

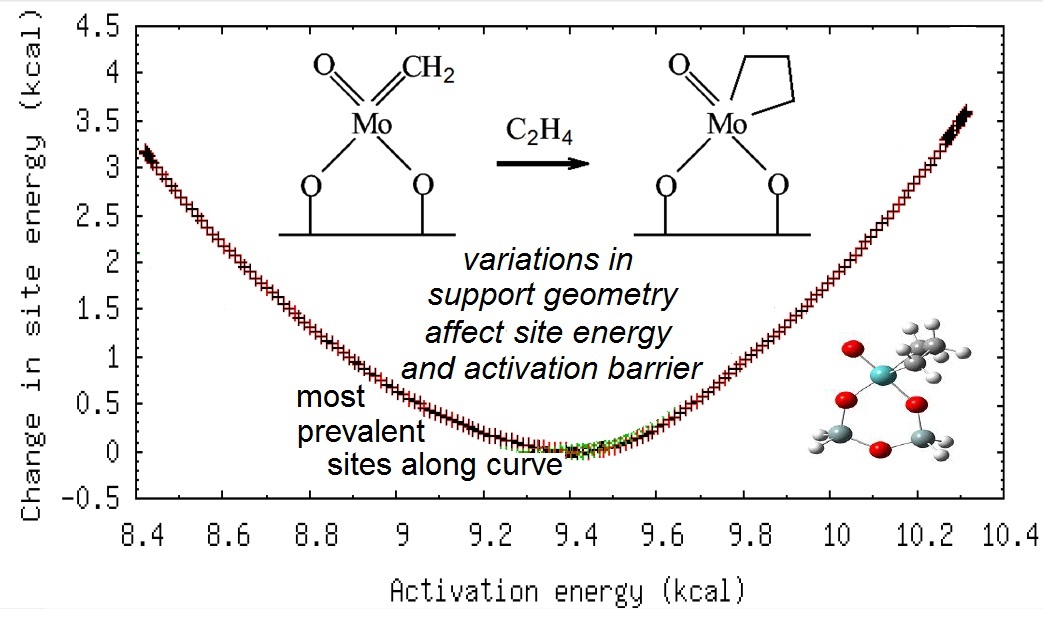
These four postulates allow us to identify the lowest energy site with a given value of a given chemical property. In this manner we can systematically understand how structure and properties are related. Figure 1 depicts the information that we can obtain from this strategy. Our work takes an important step towards resolving the longstanding difficulty with modeling amorphous materials.

	Figure 1: Depicting a manifold of sites A with the lowest energy EA for each value of a chemical property l(xp) where xp are the coordinates of the fixed peripheral atoms in the model of the solid site.

II. COMPUTATIONAL METHODS

Chemical properties are often differences between a system in two different states. For our purposes chemical properties of interest will all be energies. Activation barriers are of special interest because they are directly related to catalyst activity. To identify sites with specific activation energies we must constrain activation energy itself. This represents a more challenging calculation than familiar constrained optimization problems and transition state optimizations which are implemented in commercial electronic structure packages. Minimizing the energy with fixed bond lengths or angles is a fairly straightforward task. More challenging are seam minimizations which minimize the energy with high and low spin configurations at the same energy.

The constraint on activation energy is even more challenging. To properly define activation energy for a solid, we must also constrain the peripheral atoms of the cluster model to be the same in the two states. An activation energy constraint then involves a fixed energy difference between two different optimized states of the system, the initial state, and the transition state. The chemical property constraint is therefore a nested constrained optimization:

1)      The transition state and reactant configuration are both optimized within the peripheral atom constraints. The peripheral atom positions must be identical between the two states.

2)      The peripheral atom positions must be optimized to find the lowest reactant state energy subject to a given activation barrier (chemical property).

We have developed a sequential quadratic programming framework to solve this constrained optimization problem efficiently.

We use a reduced energy landscape formalism to give the optimized energies of states A (reactant) and B(transition state) in terms of their common peripheral atom coordinates x_p. A quadratic expansion followed by a Schur transformation gives effective gradients and second derivative matrices with respect to the reduced space of peripheral coordinates only. The result is a quadratic expansion of the reduced potential energy landscape. In the reduced space, the constrained optimization problem becomes more tractable, with the constraint and the objective function involving the same coordinates.

III. EXAMPLE

Handzlik[5] studied olefin metathesis on by isolated Mo atoms on amorphous SiO2. To model the amorphous SiO2 surface he used crystoballite (a crystalline SiO2 polymorph) with various degrees of dehydroxylation and reconstruction. Handzlik used a complex QM/MM model of the active site surrounded by the solid matrix with a total of 10 different versions of the active site. In keeping with our second postulate (2), Handzlik found different results from the different models. Our framework, as shown below, captures similar variations in the activation energy using only a small cluster model with relatively simple QM calculations and without using a crystalline model system.

[1] F. Haase and J. Sauer, J. Am. Chem. Soc. 117, 3780, (1995).

[2] J. F. Haw, et al. J. Am. Chem. Soc. 116, 7308, (1994).

[3] S. A. Zygmunt, et al., J. Phys. Chem. B, 104, 1944, (2000).

[4] N. Hansen, et al., J. Phys. Chem. C. 112, 15402, (2008).

[5] J. Handzlik, J. Phys. Chem. C. 111, 9337 (2007).

[6] J. Bronkema and A. Bell, Catalysis Letters, 122, 1 (2008).

[7] A. W. Moses, et al. J. Am. Chem. Soc. 129, 8912 (2007).

[8] A. W. Moses, et al. Organometallics, 25, 2157 (2006).