www.acsprf.org

This project aims to develop and apply molecular simulation methods that can aid in the prediction of crystalline polymorphs. Prediction of stable crystalline polymorphs should be completed by examining the relative free energies of candidate structures. In practice this is almost always done by examining the lattice energy alone, ignoring entropic contributions to the free energy. The error incurred with this procedure is generally considered to be of the order of the difference between candidate structures, but nevertheless the practice persists because it is inconvenient to consider the entropy rigorously, and approximate methods that introduce entropy tend not to lead to greater success in predicting the observed polymorphs. Such applications leave open the question as to whether failure of the prediction is due to inadequacies of the molecular model, or due to the approximations introduced to estimate the free energy. A major goal of this work is to establish the significance of the entropy (and its neglect) as a source of error in polymorph prediction efforts.

Rigorous methods to compute the free energy are seldom applied because they are tedious and computationally intensive. Thus a major component of this work is the development and/or improvement of such methods. Granted that molecular simulation is required to render a good free-energy value, we aim to develop methods that require as few simulations as possible. Accordingly, the approach we developed is based on a system of coupled harmonic oscillators combined with free-energy perturbation or thermodynamic integration.

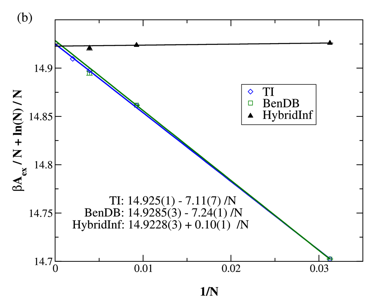
Perturbation methods can be effective if applied to systems with sufficiently few molecules. The penalty for doing so is incurring finite-size effects that introduce new errors that tend to defeat the purpose of the calculation. In this work we have made an observation that circumvents this problem. In particular, we have found that the correction to the harmonic reference (the quantity that is most challenging to calculate) is virtually independent of system size. This suggests a hybrid technique in which perturbation  is applied to a small system and the result added to a large-system harmonic reference to obtain a good estimate of the correct large-system free energy. The behavior is exemplified in FIG 1.

FIG. 1. Excess free energy for soft-sphere model evaluated with various methods, as a function of the system size used in the calculation (with infinite system a zero of abscissa) at kT/ ε = 0.5, with ρσ³  = 1.256. The notation HybridInf indicates hybrid method in which harmonic free energy extrapolated to infinite size is used, with correction from smaller system sizes (32, 108 and 256 particles), as plotted. Non-hybrid alternatives are shown in other lines, and exhibit a much greater system size dependence.  

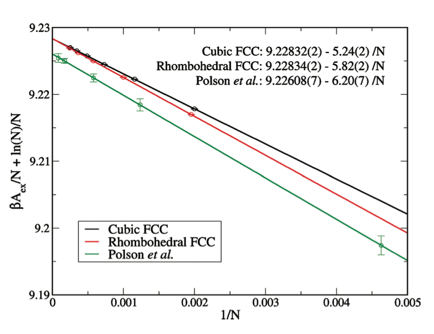
In a separate development, we formulated a method for evaluation of free-energy differences with temperature that is highly precise, accurate, and efficient.  We have applied the method to evaluate free energies for soft-sphere models with unprecedented precision, and subsequently we employed the method to compute the coexistence line for the alpha and beta forms of solid nitrogen. We call the method harmonically-targeted temperature perturbation (HTTP), and involves coupling a free-energy perturbation in temperature with harmonically-based atomic displacements that aid the perturbation calculation. The method is such that if it were applied to a true harmonic crystal, it would yield exact results, and consequently in practice the calculation accumulates noise only to the degree that the crystal is anharmonic.  The performance of the method is shown in FIG 2, which compares results from the HTTP method to the best data available previously.  It should be noticed both that we corrected a small error in the previous result, and we obtain free energies with much greater precision, as indicated by comparison of the error bars.

FIG. 2. Convergence of free energy with system size for soft-sphere model, comparing new HTTP method with literature data of Polson et al. [J. Chem. Phys. 112, 5339 (2000)]. HTTP method is applied to systems with two geometries for periodic boundaries, and agree in the infinite-system limit (y-axis intercept).

In addition we have computed virial coefficients for the soft-sphere models that were used to develop these simulation methods, obtaining results that are an order of magnitude more precise than previously established, and going one order in density higher (up to r⁸). We use the free-energy determined from the virial equation to describe the fluid, and connect to the solid-phase free-energy results described above to establish more accurate values for the solid-fluid transition point (i.e., melting or freezing point).

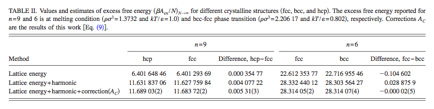
Our ultimate interest is in polymorph transitions, and we have used our solid-phase free energy data to examine its ability to capture this behavior in the soft-sphere model. We have taken special interest in the contributions to the free energy from the lattice energy by itself, the harmonic contribution, and the anharmonic correction that is the focus of this work.  Data are summarized in the following table for two soft-sphere models (indicated as n = 9 and n = 6). The latter is known to exhibit a fcc-bcc polymorphic transition, and the table shows that the contributions beyond the lattice energy are significant in establishing this behavior.

The soft-sphere model served as a useful starting point for these studies, but has anomalies that make it unsuitable as a basis for general conclusions about methods or phenomena. We closed our studies here by applying these methods to a realistic model for nitrogen molecules, looking in particular at its polymorphic behavior and the relevance of entropic effects in producing and locating it. These results now set the stage for the application of these methods in other contexts, and the formulation of robust methods for polymorph prediction.

With respect to human-resource development, this project contributed to the graduate education of one student in the Kofke group.  This student completed his PhD in summer of 2011 and he is now employed by a company where he is developing software for physics- and engineering-oriented applications.