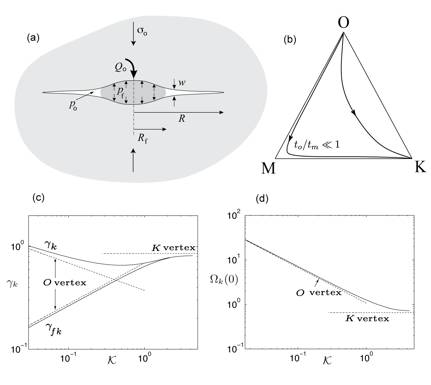
The research deals with the propagation of hydraulic fractures in impermeable elastic media and focuses on two critical aspects of this evolution problem: (i) the factors influencing the fluid lag, which is the distance between the moving crack edge and the advancing front of the fracturing fluid (Fig 1a) and (ii) the nature of the tip asymptotics when the fluid lag has vanished.  The research has both a theoretical and an experimental component.

Propagation of a radial fracture caused by injection of a Newtonian fluid at a constant volumetric rate is characterized by two time scales, t_o and t_m, that can each be associated with a physical transition the fracture makes in its lifetime. Namely, t_o gives a measure of the time for which the fluid pressure in the fracture is sufficiently large relative to the far-field confining stress so that the fracture can grow with a significant lag between the fluid and fracture fronts in spite of the clamping that the confining stress imposes on the lag region. The timescale t_m, on the other hand, gives a measure of how long it takes for the fracture to transition from an early time regime characterized by large viscous dissipation, to a large time regime where the effect of viscous dissipation is so small that the internal fluid pressure can be taken as uniform along the fracture. The triangular parametric space OMK (Fig. 1b) gives a useful way of visualizing this evolution. In this representation, fractures begin with time t=0 at the O-vertex and eventually arrive, when time is much larger than both t_o and t_m, at the K-vertex. The evolution of the fracture during its transition between the O- and the K-vertex depends on the ratio t_o/t_m. In particular, if this ratio is much smaller than 1, the fracture will pass very close to the M-vertex before proceeding to the K-vertex.  The evolution of  the fracture radius g_k and the radius of the fluid front g_fk along the OK-edge, as a function of the evolution parameter K=(t/t_m)^1/9, is shown in Fig. 1c, and the evolution of the crack opening W_k at the center of the fracture is plotted in Fig. 1d.  Note that both g_k and g_fk have to be multiplied by a scaling factor proportional to (t/t_m)^2/5 and W_k by a factor proportional to (t/t_m)^1/5 to retrieve the physical quantities.  The results shown in Figs 1c and 1d were computed with an implicit algorithm, which tracks the two moving fronts.

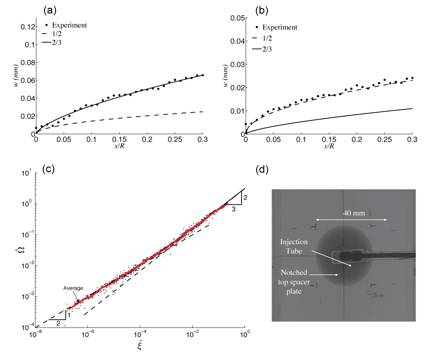
Along the MK-edge, the fluid lag is non-existent.  This edge of the parametric space is practically significant for the stimulation of hydrocarbon reservoirs by hydraulic fracturing as t_o  is effectively very small compared to the treatment time for deep fractures. Hence, the M-vertex is not only the small time solution but often characterizes the whole treatment as the pumping time is usually small compared to t_m. Importantly, the nature of the tip asymptotics changes as the fracture evolves from the M- to the K-vertex. Namely,  the crack opening w behaves near the tip as w ~ s^2/3 (with s denoting the distance from the tip) near the M-vertex, reflecting the dominance of viscous dissipation (Fig. 2a). On the other hand, w ~ s^1/2  according to linear elastic fracture mechanics near the K-vertex (Fig. 2b); this familiar asymptotic form reflects the dominance of dissipation associated with the breaking of material bonds.  A universal solution that captures the transition from the 2/3 to the 1/2 asymptote is shown in Fig 2c. These complex tip asymptotics are important for modeling hydraulic fracture growth, as it has been demonstrated that accurate and efficient computational schemes result when these conditions are imposed via an asymptotic solution that appropriately accounts for the coupled near-tip behavior.

Laboratory experiments, aimed at verifying theoretically derived asymptotic solutions, were performed by injecting glycerin or glucose at a constant rate into 200 x 200 x 150 mm Polymethyl Methacrylate (PMMA) or glass specimens so as to produce circular fractures. The fluid for these experiments contained dye which enabled the fracture opening to be measured over the tip region based on the intensity drop associated with light passing through the fluid-filled fractures (Fig 2d). Strong agreement between the experimental and theoretical predictions of fracture tip opening (Figs 2a, 2b, and 2c) confirms not only that the near-tip region is indeed characterized by multiple scales, but also that the asymptotic solution is able to accurately predict the observed physical behavior.